Besaran vektor atau sering disebut dengan vektor yaitu besaran fisika yang mempunyai besar dan arah.
Contoh besaran vektor adalah perpindahan, kecepatan, percepatan, gaya dan lain sebagainya.
Vektor ini mempunyai beberapa sifat, yang diantaranya adalah bisa dipindahkan, dijumlahkan, dikurangkan, diuraikan dan dikalikan.
Terus, gimana sih metode buat penjumlahan vektor itu sendiri? Pengin tahu?
Nah, berikut ini ada beberapa metode penjumlahan vektor yang perlu diketahui. Simak langsung yuk!
Metode Grafis Penjumlahan Vektor

Metode grafis ini perlu sketsa yang tepat skalanya, jadi diperlukan mistar dan busur derajat buat mengukurnya.
Metode grafis sebenarnya sangat praktis, tapi memerlukan ketelitian dalam menggambar dan melakukan pengukuran panjang resultan dan sudutnya.
Beberapa vektor bisa dijumlahkan menjadi sebuah vektor yang disebut dengan resultan vektor.
Dengan penjumlahan secara grafis, resultan vektor dapat diperoleh dengan beberapa metode yaitu metode segitiga, metode jajargenjang, dan metode poligon dan lainnya.
1. Metode Segitiga
Metode segitiga yaitu cara penjumlahan dua buah vektor secara grafis di mana salah satu titik tangkap dipindahkan ke ujung vektor yang lain, lalu ditarik garis lurus dari pangkal ke ujung vektor tersebut.
Garis dari pangkal ke ujung dua vektor adalah hasil penjumlahan vektro atau disebut dengan resultan dari dua vektor tersebut.
Ada langkah buat penjumlahan sebuah vektor dengan metode segitiga, seperti gambar berikut ini.
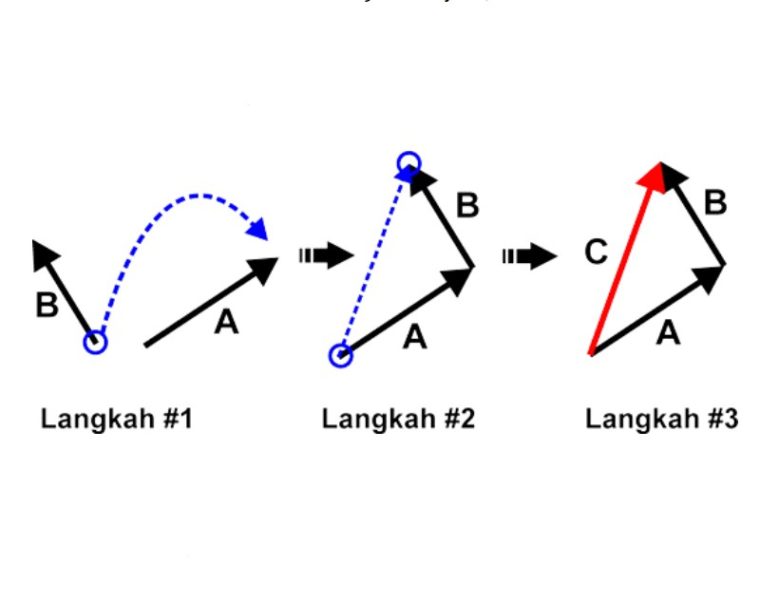
Dari sebuah gambar diatas, maka kamu ketahui kalo vektor C yaitu hasil dari penjumlahan vektor A dan vektor B. Jadi, kamu juga bisa menyebut C sebagai vektor resultan.
Secara matematis, penjumlahan vektor A dan vektor B ini bisa dituliskan sebagai berikut dibawah ini:
A + B = C atau C = A + B
Dalam metode segitiga ini, buat menentukan vektor mana yang termasuk resultan dari penjumlahan dua vektor bisa dilakukan dengan memakai teknik seperti dibawah ini.
Vektor Resultan = Ujung bertemu ujung dan pangkal bertemu pangkal.
Jadi, kalo ada 3 buah vektor yang membentuk bangun segitiga, buat menentukan mana vektor yang termasuk vektor resultan yaitu dengan melihat ujung dan pangkal vektor-vektornya.
Kalo ada sebuah vektor yang ujungnya bertemu ujung vektor lain dan pangkal vektor bertemu dengan pangkal vektor yang lain, maka udah dipastikan kalo vektor tersebut yaitu vektor resultan.
Lalu, buat menentukan persamaan resultan vektornya. Kamu tulis penjumlahan vektor dimulai dari vektor yang pangkalnya bertemu pangkat vektor lain yang jadi resultannya.
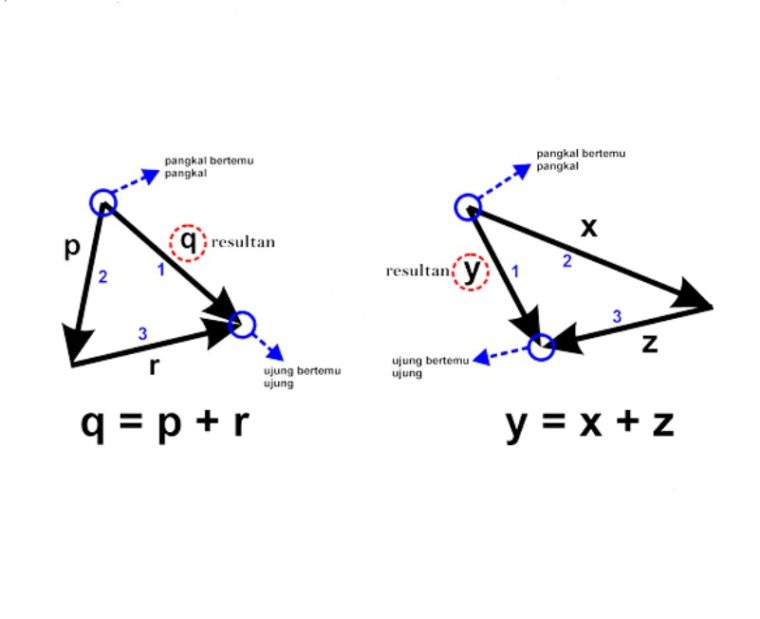
Pada penjumlahan vektor p, q dan r di atas, vektor yang pangkal dan ujungnya bertemu dengan pangkal dan ujung vektor yang lain adala adalah vektor q.
Jadi, bisa kamu katakan kalo vektor q merupakan vektor resultan atau hasil penjumlahan antara dua vektor yang lain.
Buat menuliskan persamaan resultan vektornya, vektor pertama yang harus ditulis dulu yaitu vektor q lalu vektor yang kedua yaitu vektor yang pangkalnya bertemu dengan vektor resultan, yaitu vektor p dan yang terakhir vektor sisanya yaitu r.
Nah jadi secara matematis, persamaan resultan vektornya yaitu sebagai berikut ini.
q = p + r
Dengan memakai cara yang sama, maka hasil penjumlahan antara vektor x, y, dan z bisa dituliskan dalam bentuk persamaan sebagai berikut dibawah ini.
y = x + z
2. Metode Jajargenjang
Metode jajargenjang yaitu saah satu metode grafis yang dipakai buat menjumlahkan beberapa vektor, baik itu vektor berjumlah 2 atau bahkan lebih dari itu.
Metode jajargenjang merupakan cara penjumlahan vektor dengan menghubungkan pangkal vektor yang satu ke pangkal vektor yang lainnya.
Lalu, menarik sebuah garis lurus dari pangkal kedua vektor menuju perpotongan proyeksi dari masing – masing vektor.
Garis ini merupakan verktor resultan. Berikut, ada langkah-langkah buat menjumlahkan vektor dengan metode jajargenjang pada gambar berikut ini.
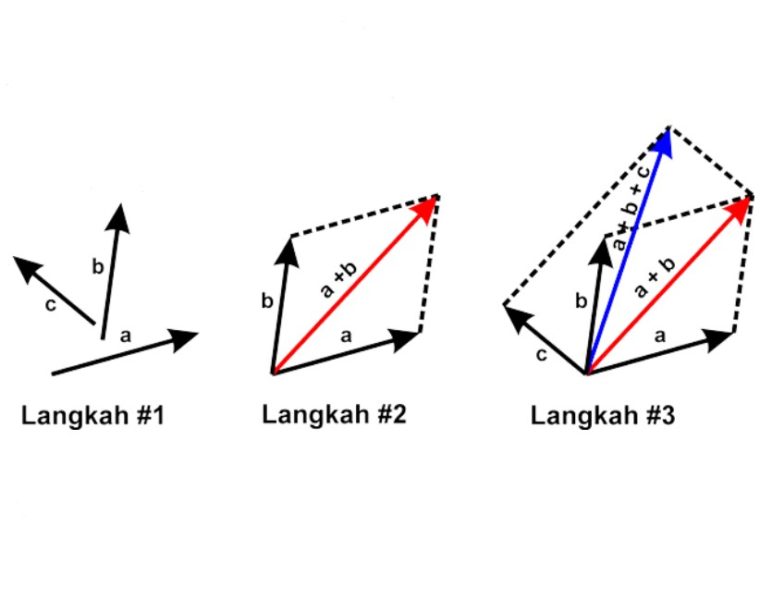
Dari gambar diatas, penjumlahan vektor dengan memakai metode jajargenjang dilakukan secara bertahap, yaitu dengan menjumlahkan 2 vektor dulu.
Kemudian, vektor resultan dari 2 vektor sebelumnya dijumlahkan dengan vektor ketiga dan seterusnya. Contohnya ada dibawah ini:
- Vektor (a) dijumlahkan dengan vektor (b), maka hasilnya adalah vektor (a+b) garis berwarna merah.
- Vektor (a+b) dijumlahkan dengan vektor (c), maka hasilnya adalah vektor (a+b+c) garis berwarna biru.
Nah, cara itu terus dilakukan sampai pada penjumlahan vektor yang terakhir.
3. Metode Poligon
Metode poligon ini sebenarnya masih sama dengan metode segitiga, cuma aja jumlah vektor yang dijumlahkan lebih banyak.
Metode poligon yaitu cara penjumlahan tiga atau lebih vektor secara grafis dengan saling menghubungkan pangkal vektor ke ujung vektor lainnya sampai vektor terakhir.
Lalu, ditarik garis lurus dari pangkal vektor pertama menuju ujung vektor terakhir. Jadi, terbentuklah bangun segi banyak atau yang sering disebut dengan poligon.
Dibawah ini, ada langkah – langkah penjumlahan vektor dengan memakai metode poligon seperti gambar berikut ini.
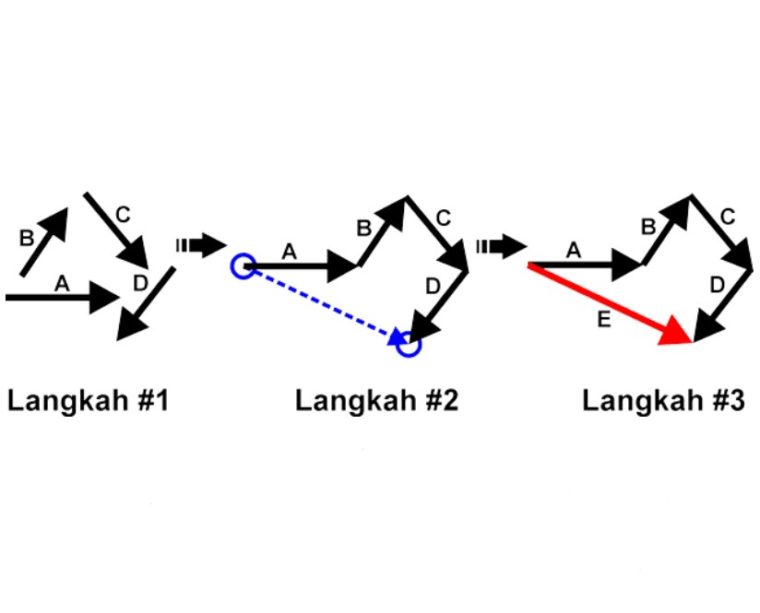
Perlu diingat! Kalo dalam memindahkan pangkal vektor ke ujung vektor yang lain, kamu gak boleh mengubah besar dan arah vektornya karena panjang dan arah anak panah harus tetap.
Dari sebuah gambar yang ada diatas, hasil penjumlahan vektor A, B, C, D dan E bisa dituliskan seperti yang ada dibawah ini:
E = A + B + C + D
E yaitu vektor resultan dari penjumlahan vektor A, B, C, dan D. Sama seperti metode segitiga, buat menentukan vektor mana yang termasuk resultan dari penjumlahan beberapa vektor, kamu bisa pakai teknik seperti ini:
Vektor Resultan = Ujung bertemu ujung dan pangkal bertemu pangkal.
Jadi pada metode poligon, buat menentukan vektor mana yang termasuk resultan yaitu dengan melihat ujung dan pangkal vektor-vektornya.
Kalo ada sebuah vektor yang ujungnya bertemu dengan ujung vektor lain dan pangkalnya juga bertemu dengan pangkal vektor yang lain, maka vektor itu adalah vektor resultan.
Lalu buat menuliskan persamaan resultan vektornya, tulis penjumlahan vektor mulai dari vektor yang pangkalnya bertemu dengan pangkal vektor yang jadi resultannya.
Nah, kamu coba perhatikan gambar yang ada dibawah ini nih.
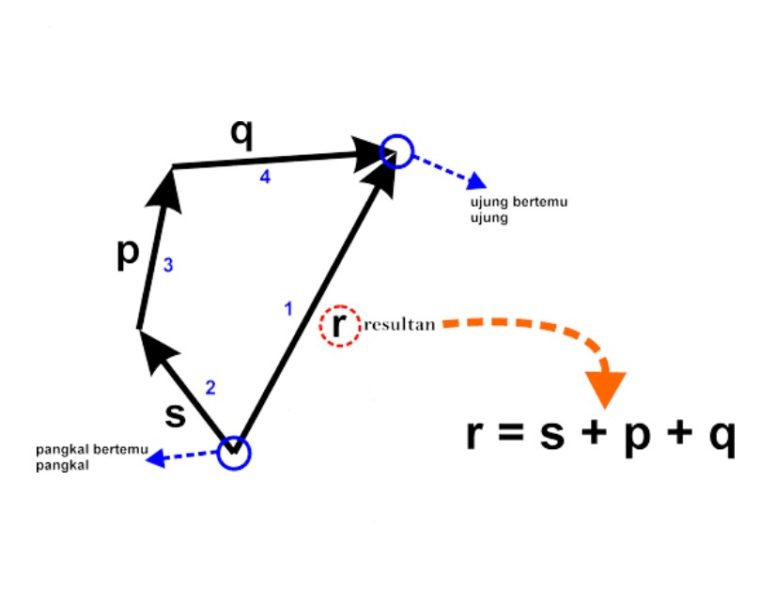
Pada penjumlahan vektor p, q, r dan s. Vektor yang pangkal dan ujungnya bertemu dengan pangkal dan ujung vektor yang lainnya yaitu vektor (r).
Jadi, bisa dikatakan kalo vektor r merupakan vektor resultan.
Buat menuliskan penjumlahan vektornya, vektor pertama yang ditulis yaitu vektor r lalu vektor kedua yaitu vektor yang pangkalnya bertemu dengan pangkal vektor resultan, yaitu vektor s.
Dengan demikian seterusnya, sampai jadi persamaan resultannya bisa kamu tuliskan seperti ini:
r = s + p + q
Dalam metode poligon, karena vektor yang dijumlahkan ada banyak. Maka, kamu bisa menemui lebih dari satu vektor resultannya.
Hal ini vektor yang jadi resultannya ada lebih dari satu (bukan vektor resultan tunggal). Contohnya, seperti gambar berikut ini.
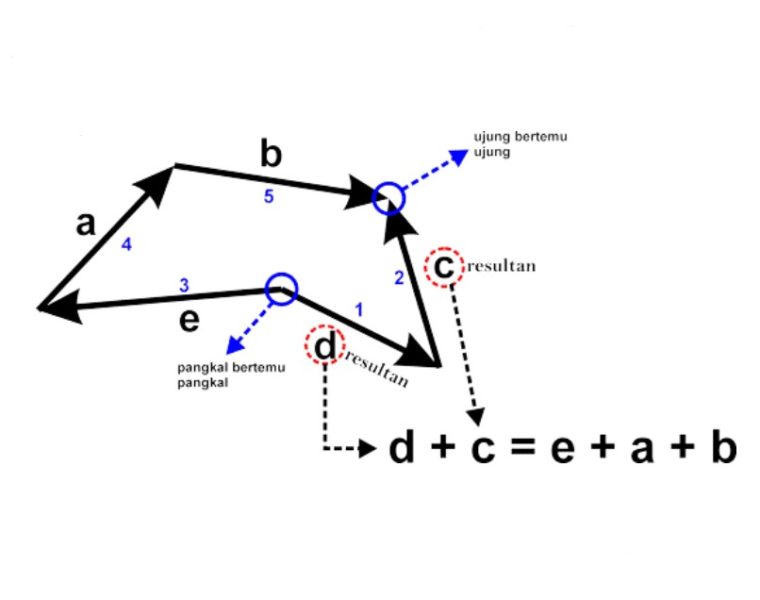
Perhatikan gambar diatas ini, ujung vektor (c) bertemu dengan ujung vektor (b) dan pangkal vektor (d) bertemu dengan pangkal vektor (e).
Karena, ujung bertemu ujung dan pangkal bertemu pangkal, maka bisa dikatakan vektor (d) dan (c) yaitu vektor resultannya.
Dengan itu, jumlah vektor (d) dan (c) sama dengan jumlah vektor (e, a dan b), jadi persamaan resultan vektornya bisa kamu tuliskan sebagai berikut:
d + c = e + a + b
4. Rumus Cosinus
Rumus cosinus yaitu rumus yang dipakai buat menentukan besar resultan dua buah vektor yang mengapit sudut tertentu.
Misalnya, ada 2 buah vektor yaitu A dan B dimana satu sama lainnya mengapit sudut seperti contoh gambar yang ada dibawah ini.
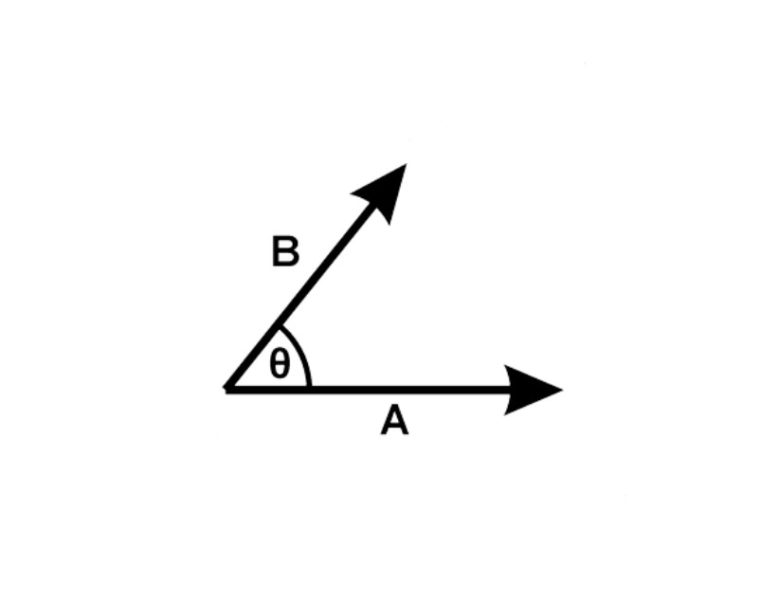
Apabila R merupakan vektor resultan atau penjumlahan dari vektor A + B, maka besar R bisa ditentukan dengan memakai rumus cosinus seperti ini:
R = √A2 + B2 + 2AB cos θ
5. Metode Penguraian
Metode penguraian disebut juga metode analitis yaitu cara menjumlahkan vektor dengan memproyeksikan vektor-vektor pada sumbu-X dan sumbu-Y diagram cartesius, lalu komponen-komponen vektor pada masing-masing sumbu dijumlahkan secara biasa.
Vektor komponen yang arahnya ke kanan atau ke atas bernilai positif, sedangkan vektor komponen yang arahnya ke bawah bernilai negatif.
Misalkan ada 6 buah vektor gaya yaitu F1, F2, F3, F4, F5 dan F6 yang masing-masing besarnya adalah 10N, 15N, 8N, 5N, 20N, dan 18N.
Apabila arah keenam vektor terhadap sumbu X positif adalah 37o, 120o, 180o, 233o, 270o, dan 315o, maka dengan memakai metode penguraian, langkah-langkah penjumlahannya adalah sebagai berikut.
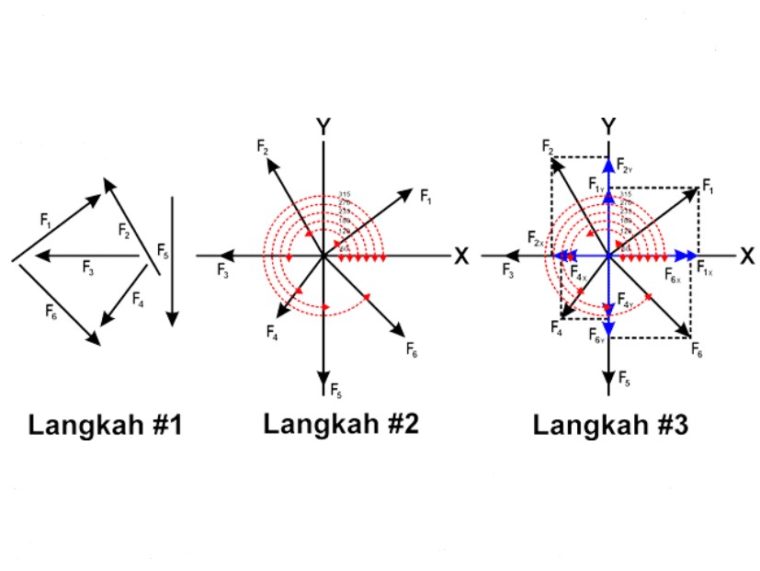
Setelah vektor komponen terbentuk seperti yang diperlihatkan pada langkah 3, saatnya kamu mulai proses perhitungan.
Hal pertama yang harus dilakukan yaitu menentukan besar masing-masing komponen dengan rumus FX = F cos α (untuk vektor komponen pada sumbu-X) dan rumus FY = F sinα (buat vektor komponen pada sumbu-Y).
Adapun besar masing – masing vektor komponen pada kedua sumbu adalah sebagai berikut.
|
Vektor komponen pada sumbu X
|
Vektor komponen pada sumbu Y
|
|
F1X = F1 cos α1 = (10)( cos 60) = 5 N
|
F1Y = F1 sin α1 = (10)( sin 60) = 8,67 N
|
|
F2X = F2 cos α2 = (15)(cos 120) = -7,5 N
|
F2Y = F2 sin α2 = (15)(sin 120) = 12,99 N
|
|
F3X = F3 cos α3 = (8)(cos 180) = -8 N
|
F3Y = F3 sin α3 = (8)(sin 180) = 0
|
|
F4X = F4 cos α4 = (5)(cos 233) = -3 N
|
F4Y = F4 sin α4 = (5)(sin 233) = -4 N
|
|
F5X = F5 cos α5 = (20)(cos 270) = 0
|
F5Y = F5 sin α5 = (20)(sin 270) = -20 N
|
|
F6X = F6 cos α6 = (18)(cos 315) = 12,73 N
|
F6Y = F6 sin α6 = (18)(sin 315) = -12,73 N
|
Setelah besar vektor komponen pada sumbu X dan Y diketahui, selanjutnya jumlahkan masing-masing vektor komponen tersebut, yaitu sebagai berikut.
|
ΣFX = F1X + F2X + F3X + F4X + F5X + F6X
ΣFX = 5 N +(-7,5 N) + (-8 N) + (-3 N) + 0 + (12,73 N)
ΣFX = -0,77 N
|
|
ΣFY = F1Y + F2Y + F3Y + F4Y + F5Y + F6Y
ΣFY = 8,67 N + 12,99 N + 0 + (-4 N) + (-20) + (-12,73 N)
ΣFY = -15,07 N
|
Selanjutnya, hasil penjumlahan keenam vektor atau besar resultan vektor bisa ditentukan dengan memakai rumus berikut.
- R = √(ΣFX)2 + √(ΣFY)2
- R = √(-0,77)2 + √(-15,07)2
- R = √0,5929 + √227,1049
- R = √227,6978 = 15, 09 N
Sedangkan, arah vektor resultannya adalah:
- tan β = ΣFY/ΣFX
- tan β = -15,07/-0,77
- tan β = 19,57
β = arc tan 0,0511 = 87o terhadap sumbu-X horizontal.
Selisih Vektor
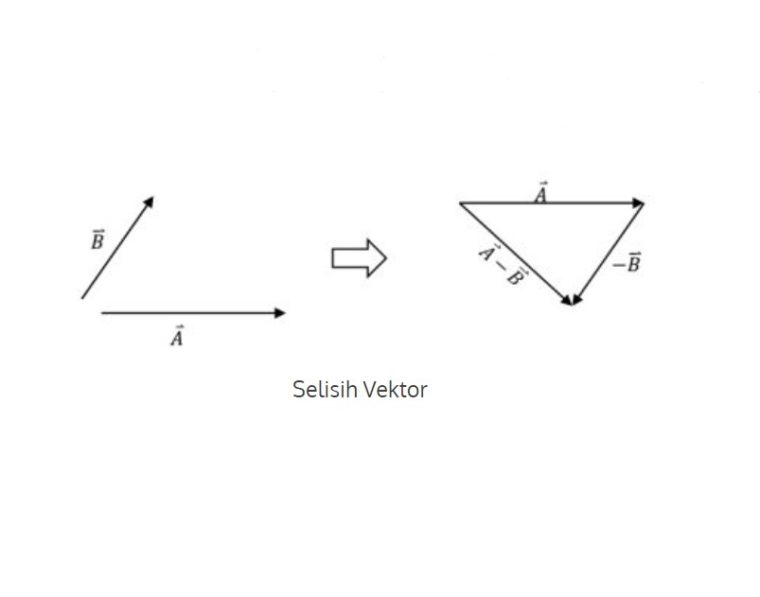
Penghitungan selisih vektor atau disebut juga dengan pengurangan vektor pada prinsipnya sama dengan penjumlahan vektor.
Cuma aja di selisih vektor, penjumlahannya dilakukan dengan vektor negatifnya. Vektor negatif merupakan vektor yang besarnya sama, tapi arahnya berlawanan.
Contoh dari selisih vektor atau pengurangan vektor adalah R = A -B atau R = A + (-B). Hal ini menunjukan kalo selisih antara vektor A dan B yaitu hasil penjumlahan vektor A dan -B, dengan -B adalah vektor yang berlawanan arah dengan B, tapi nilainya sama dengan B. Seperti gambar diatas.
Yey udah selesai belajar mengenai metode penjumlahan vektor ini! 😀


Apa itu penjumlahan vektor?