Eits, tahu gak sih kamu tentang hukum Kirchhoff? Siapa sih penemu hukum Kirchhoff itu dan terbagi menjadi berapa sih hukum Kirchhoff itu sendiri?

Pengin tahu lebih jelas dan lengkap? Langsung aja simak nih, pembahasan tentang Hukum Kirchhoff yang ada dibawah ini.

Penemu Hukum Kirchhoff

Hukum Kirchhoff yaitu dua persamaan yang berhubungan dengan arus dan beda potensial (tegangan) dalam sebuah rangkaian listrik.

Pada tahun 1845 seorang ahli fisika dari Jerman yang bernama Gustav Robert Kirchhoff (1824-1887) yang pertama kali memperkenalkan hukum kirchhoff ini.

Banyak dari rangkaian listrik sederhana (seperti gambar dibawah ini) yang gak bisa dianalisis dengan cuma mengganti kombinasi rangkaian seri dan paralel resistor dalam menyederhanakan rangkaian yang punya banyak resistor.

Tegangan jatuh pada R1 dan R2 tidaklah sama, karena adanya ggl E2. Jadi, rangkaian kedua resistor ini gak paralel juga bukan rangkaian seri, karena arus yang mengalir pada kedua resistor gak sama.

Tapi, ada hukum yang berlaku pada rangkaian yang mempunyai arus tetap (tunak). Hukum ini merupakan hukum Kirchhoff I dan Kirchhoff II.

Hukum Kirchhoff I

Hukum kirchhoff 1 atau sering disebut dengan Hukum Arus Kirchhoff atau Kirchhoff’s Current Law (KCL), karena hukum ini memenuhi kekekalan muatan.

Hukum kirchhoff 1 ini, diperlukan buat rangkaian yang multisimpal yang mengandung titik-titik percabangan saat arus mulai terbagi.

Pada keadaan tunak, gak ada akumulasi muatan listrik pada setiap titik didalam rangkaian. Makanya, jumlah muatan yang masuk didalam setiap titik akan meninggalkan titik tersebut dengan jumlah yang sama.

Bunyi Hukum Kirchhoff I:

Jumlah arus listrik yang masuk lewat titik percabangan dalam suatu rangkaian listrik, sama dengan jumlah arus yang keluar lewat titik percabangan tersebut.

Rumus hukum Kirchhoff I:

ΣI_masuk = ΣI_keluar

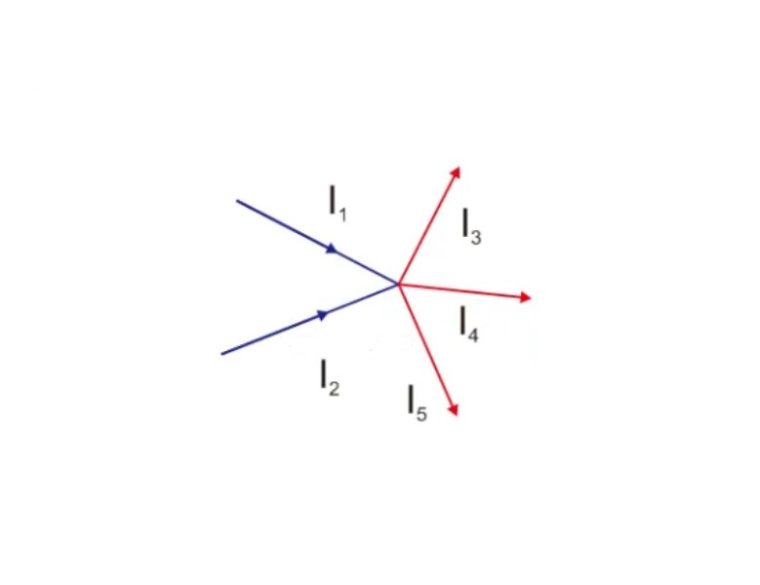
Contohnya, pada gambar diatas menunjukan suatu titik percabangan dari 5 buah kawat yang dialiri arus I1, I2, dan I3. Dalam rentang waktu Δt, muatan q1 = I1Δt mengalir lewat titik percabangan dari arah kiri.

Dalam rentang waktu Δt juga, muatan q2 = I2Δt dan q3 = I3Δt bergerak ke arah kanan meninggalkan titik percabangan.

Karena, muatan tersebut bukan berasal dari titik percabangan dan gak juga menumpuk pada titik tersebut dalam keadaan tunak, maka muatan akan terkonservasi di titik percabangan tersebut, yaitu:

I1 = I2 + I3

Hukum Kirchhoff II

Hukum Kirchhoff 2 ini atau sering disebut dengan Hukum Tegangan Kirchhoff atau Kirchhoff’s Voltage Law (KVL).

Karena, pada kenyataannya beda potensial diantara dua titik percabangan dalam satu rangkaian pada keadaan tunak adalah konstan. Hukum ini adalah bukti dari adanya hukum konservasi energi.

Kalo kamu punya suatu muatan Q pada sembarang titik dengan potensial V, dengan demikian energi yang dimiliki oleh muatan tersebut yaitu QV.

Lalu, kalo muatan mulai bergerak melintasi simpal tersebut, maka muatan yang kamu miliki akan dapat tambahan energi atau kehilangan sebagian energinya saat lewat resistor baterai atau elemen lainnya.

Tapi, saat kembali ke titik awalnya, energinya akan kembali menjadi QV.

Bunyi Hukum Kirchhoff 2:

Pada setiap rangkaian tertutup, jumlah beda potensialnya harus sama dengan nol (0).

Rumus Hukum Kirchhoff 2:

Σε + ΣI. R = 0

Contohnya, kamu bisa lihat pada gambar diatas tadi, dua baterai yang berisi hambatan r1 dan r2 serta ada juga 3 hambatan luar. Kamu akan bisa menentukan arus dalam rangkaian tersebut sebagai fungsi GGL dan hambatan.

Jumlah rangkaian tertutup (loop) dalam satu rangkaian listrik bisa satu atau lebih.

Dalam pemakaian hukum Kirchhoff II pada rangkaian tertutup ada beberapa aturan yang harus kamu ketahui nih, diantaranya yaitu:

• Pilih loop buat masing-masing lintasan tertutup dengan arah tertentu, bisa bebas tapi kamu usahakan buat searah dengan arus listrik yang mengalir.
• Kuat arus bertanda positif (+), kalo searah dengan arah loop yang ditentukan dan bertanda negatif (-), kalo berlawanan dengan arah loop yang udah kamu tentukan di angka 1.
• Apabila saat mengikuti arah loop, kutub positif (+) sumber tegangan dijumpai lebih dulu dari pada kutub negatifnya (-) mana GGL (ε) bertanda positif. Sebaiknya, kalo kutub negatif (-) dijumpai lebih dulu dari kutub positif (+) maka nilai GGL (ε) negatif.
• Kutub positif (+) disimbolkan dengan garis panjang dan kutub negatif adalah garis pendek.

a. Rangkaian dengan Satu Loop

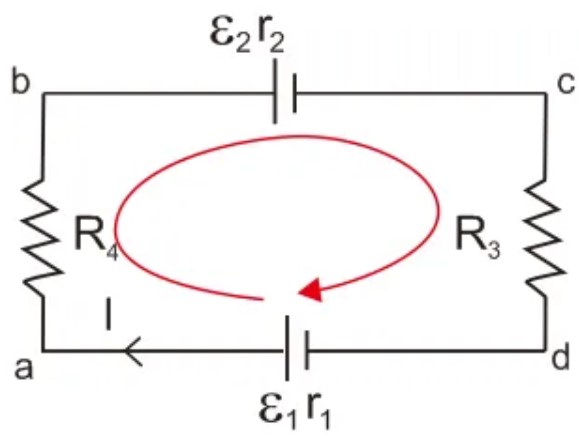
Dalam rangkaian dengan memakai satu loop, maka kuat arus yang mengalir adalah sama, sebesar 1. Kalo rangkaian diatas, kamu buat loop a-b-c-d maka sesuai pada hukum Kirchhoff II berlaku dengan persamaan berikut ini.

Σε + ΣI. R = 0
(ε₁ – ε₂) + I (R₄ + r₂ + R₃ + r₁) = 0

Contoh Soal!

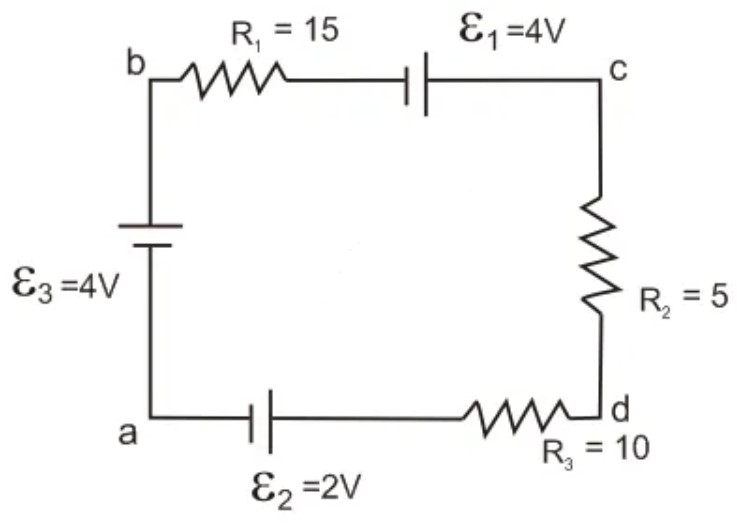
1. Coba kamu perhatikan gambar yang ada diatas ini. Dan kamu tentukan:

• Kuat arus yang mengalir lewat rangkaian tersebut?
• Tegangan antara a dan b.

Jawaban:

Diketahui:

• R1 = 15
• R2 = 5
• R3 = 10
• ε1 = 4 V
• ε2 = 2 V
• ε3 = 4V

Ditanya:

• Kuat arus yang mengalir lewat rangkaian tersebut?
• Tegangan antara a dan b.

Jawab:

a. Arah kuat arus kita anggap dulu berlawanan dengan arah loop?

• Σε + ΣI. R = 0
• ε₃ – ε₂ + ε₁ – I (R₁ + R₂ + R₃) = 0
• 4 – 2 + 4 – I (15 + 5 + 10) = 0
• 6 – 30I = 0
• 30I = 6
• I = 6/30 = 1/5 = 0,2 A

b. Tegangan antara a dan b (Vab)

Kalo lewat jalur a-b-c-d (panjang)

• V_ab = ε₃ – ε₂ – I (R₃ + R₂) (I negatif karena berlawanan dengan arah I total)
• V_ab = 4-2 – 0,2 (10 + 5)
• V_ab = 2 – 0,2 (15)
• V_ab = 2 – 3 = -1 V

Kalo lewat jalur a-b (pendek)

• V_ab = -ε₁ + I R₁ ( I positif karena searah dengan I total)
• V_ab = – 4 +  0,2 (15)
• V_ab = -4 + 3 = -1 V

Jadi tegangan antara titik  a dan b (V_ab) = -1 V

b. Persamaan dengan Dua Loop atau Lebih

Pada rangkaian dengan dua loop atau lebih secara prinsip, bisa dipecahkan seperti pada rangkaian satu loop.

Cuma, perlu kamu perhatikan juga kuat arus pada setiap percabangannya. Coba perhatikan langkah-langkah dibawah ini.

• Tentukan kuat arus (simbol dan arahnya) pada setiap percabangan yang dianggap perlu.
• Sederhanakan susunan sei-paralel resistor kalo memungkinkan.
• Tentukan arah masing-masing loop.
• Tulislah persamaan setiap loop dengan memakai hukum Kirchhoff II.
• Tulislah persamaan arus, buat tiap titik percabangan dengan memakai hukum Kirchhoff.

Coba kamu perhatikan gambar yang ada dibawah ini.

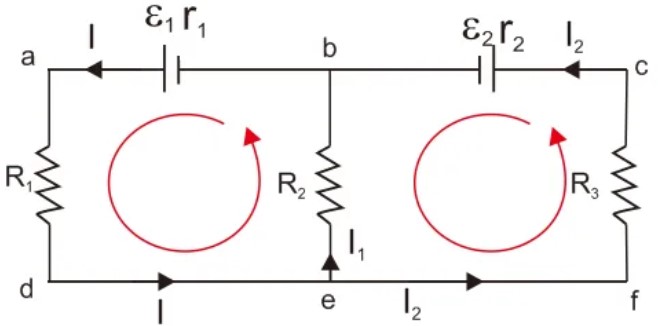
Tentukan arah dan simbol kuat arusnya!

pada b-a-d-e → I

pada e-f-c-b → I2

pada eb → I1

Kamu lihat dititik b atau c (silahkan pilih) dengan hukum Kirchhoff I

I = I1 + I2

Kamu bisa lihat masing-masing loop dengan hukum Kirchhoff II

Loop I: -ε1 + I(r₁+R₁) + I₁(R₂) = 0  (ada dua arus pada loop I)

Loop II: ε₂ – I₁.R₂ + I₂ (R₃ + r₂) = 0 (ada dua arus pada loop 2, I1 berlawanan dengan arah loop)

Contoh Soal!

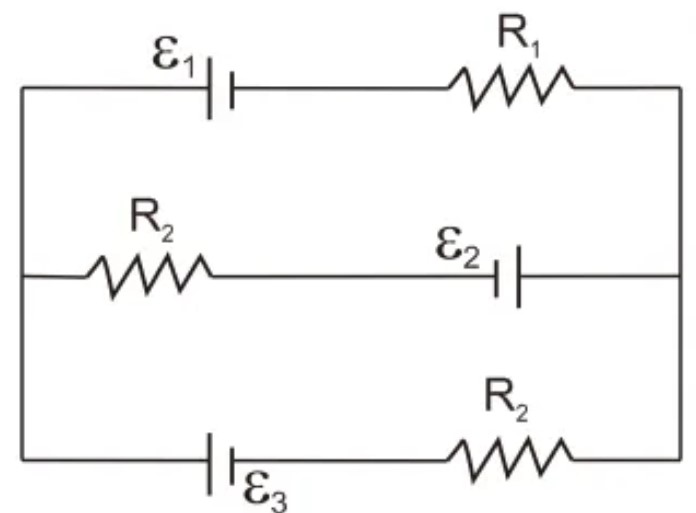
Kamu perhatikan gambar yang ada diatas ini!

Jawaban:

Diketahui:

• R₁ = 12 ohm
• R₂ = 6 ohm
• R₃ = 6 ohm
• ε₁ = 16 V
• ε₂ = 8 V
• ε₃ = 10 V

Ditanya: Kalo hambatan dalam sumber tegangan diabaikan, berapa kuat arus yang melalui R2?

Jawab:

Loop I :

• -ε₁ – ε₂ + I₁.R₂ + I.R₁ = 0
• -16  – 8 + I₁.6 + I. 12 = 0
• -24 + 6I₁ + 12 I = 0
• 6I₁ + 12I = 24
• I₁ + 2I = 4 _{….. (ketemu persamaan I)}

Loop II :

• ε₂ + ε₃ -I₁.R₂ + I₂.R₃ = 0
• 8 + 10 – I₁.6 + I₂.6 = 0
• 18 – 6I₁+ 6I₂ = 0
• -6I₁+ 6I₂ = – 18
• -6(I₁ – I₂) = 18
• I₁ – I₂ = 3
• I₁ = 3 +I_{2 …. (ketemu persamaan II)}

Kamu kombinasikan persamaan I dan II

• I1 + 2I = 4
• I1 + 2(I1 + I2) = 4
• 3I1 + 2I2 = 4 → kamu masukan persamaan II
• 3(3 + I2) + 2I2 + 4
• 9 + 3I2 + 2I2 = 4
• 5I2 = -5
• I2 = -1 A
• I1 = 3 + I2 = 3 + (-1) = 2 Ampere

Jadi, dengan memakai hukum Kirchhoff I dan hukum Kirchhoff II kita bisa menemukan kuat arus yang melalui R₂ adalah 2 Ampere.

Kesimpulan (Infografis)

Itu tadi diatas, penjelasan lengkap mengenai Hukum Kirchhoff I dan hukum Kirchhoff II dan beberapa contoh soal dengan pembahasannya.

Semoga bisa bermanfaat dan membantu kalian semua dalam membaca dan mempelajari artikel ini 😀