Dari gambar diatas, maka bisa dijelaskan:

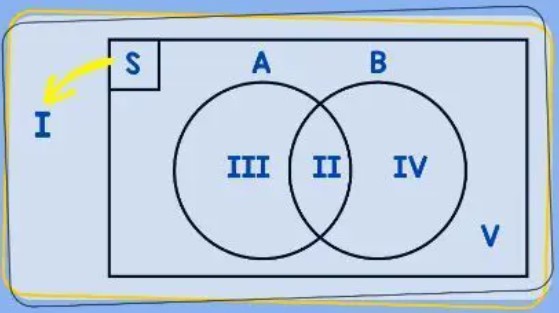
• I. Himpunan Semesta: Menggambarkan total dari anggota yang dibicarakan.
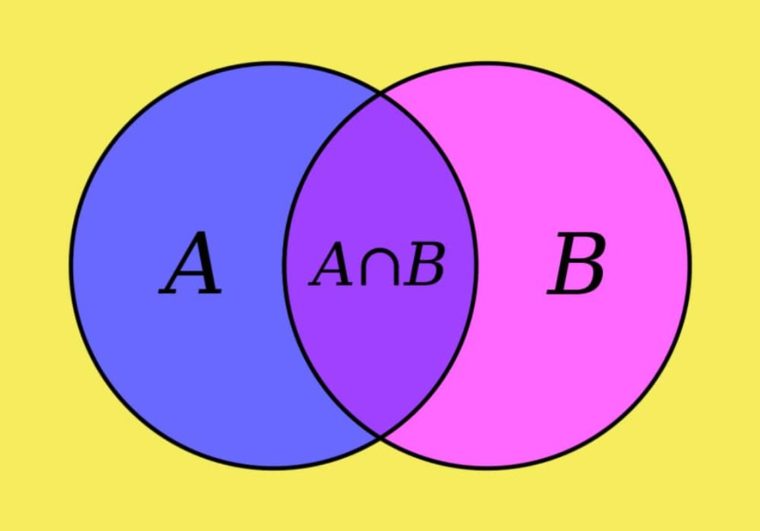
• II. Daerah yang merupakan milik himpunan A dan B (A∩B).
• III. Banyak anggota himpunan A aja (tanpa B).
• IV. Banyak anggota himpunan B aja (tanpa A).
• V. Banyak anggota semesta tetapi bukan anggota A atau B.

Aturan Penggambaran Diagram Venn

Untuk membuat suatu diagram venn, maka ada beberapa hal yang perlu kamu perhatikan, diantaranya yaitu:

• Himpunan semesta (S) dinyatakan di dalam bentuk persegi panjang. Himpunan semesta yaitu seluruh anggota himpunan yang didalamnya meliputi himpunan yang tengah menjadi fokus pembahasan.
• Himpunan lain yang menjadi fokus pembahasan udah dinyatakan dengan bentuk lingkaran atau kurva tertutup.
• Anggota pada setiap himpunan dinyatakan di dalam bentuk titik atau noktah.
• Apabila anggota himpunannya tidak terhingga, maka tiap-tiap anggota tidak perlu buat dinyatakan sebagai titik.

Supaya lebih jelas, perhatikan contoh dibawah ini:

• S = {a, b, c, d, e}
• A = {b, d, e}

Diagram venn yang sesuai dengan himpunan diatas yaitu:

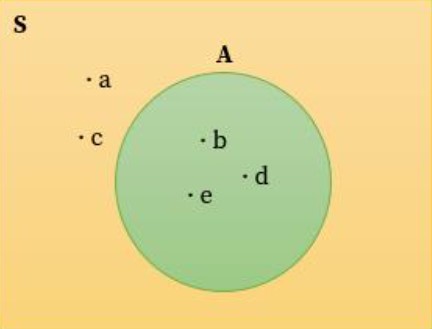
Pada contoh diagram diatas, kamu akan mengenal istilah himpunan bagian, yaitu himpunan A adalah himpunan bagian dari himpunan semesta.

Secara matematis, maka disimbolkan sebagai A ⊂ S.

Bentuk Diagram Venn

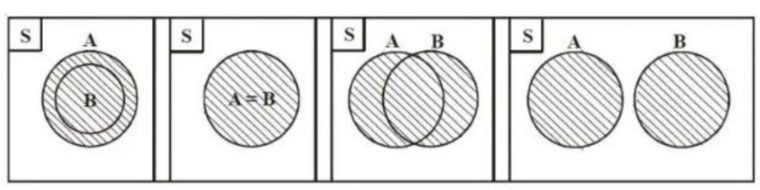
Berikut dibawah ini, ada beberapa bentuk pada diagram venn yang perlu kamu tahu, yaitu:

1. Himpunan Saling Berpotongan

Diagram satu ini digambarkan dengan dua himpunan yang saling berpotongan, karena memiliki kesamaan.

Contohnya:

Apabila ada himpunan A dan B, keduanya akan saling berpotongan kalo memiliki kesamaan, maka hal tersebut artinya anggota yang masuk kedalam himpunan A masuk juga kedalam himpunan yang B.

Himpunan A yang berpotongan dengan himpunan B bisa ditulis dengan A∩B.

2. Himpunan Saling Lepas

Himpunan A dan B bisa disebut saling lepas, apabila anggota himpunan A tidak memiliki anggota yang sama dengan anggota himpunan B.

Himpunan yang saling lepas satu ini bisa kamu tulis dengan A//B.

3. Himpunan Bagian

Himpunan A bisa juga disebut sebagai bagian dari himpunan B, kalo seluruh anggota himpunan A adalah anggota dari himpunan B.

4. Himpunan Yang Sama

Diagram venn jenis menyatakan kalo himpunan A dan B terdiri atas anggota himpunan yang sama.

Sehingga, bisa kamu simpulkan bahwasannya setiap anggota B merupakan anggota A.

Contohnya:

A = {2,3,4} dan B= {4,3,2} yaitu suatu himpunan yang sama, jadi kamu bisa menulisnya dengan A=B.

5. Himpunan Yang Ekuivalen

Himpunan A dan B disebut sebagai ekuivalen, kalo banyaknya anggota dari kedua himpunan sama.

Himpunan A ekuivalen dengan himpunan B bisa kamu tulis dengan n(A)= n(B).

Didalam diagram venn ada 4 hubungan antar himpunan yang mencangkup irisan, gabungan, komplemen himpunan dan selisih himpunan, berikut penjelasannya:

• Irisan

Irisan himpunan A dan B (A∩B) yaitu suatu himpunan yang mana anggotanya ada didalam himpunan A dan himpunan B.

Contohnya:

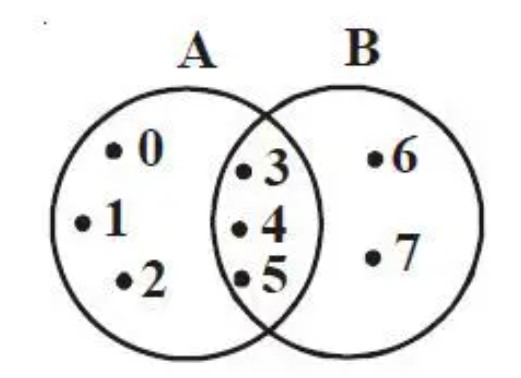
Himpunan A ={ 0,1,2,3,4,5} dan himpunan B ={3,4,5,6,7}.

Coba kamu perhatikan, kalo diantara kedua himpunan itu ada dua anggota yang sama yaitu angka 3,4 dan 5.

Nah, dari kesamaan itu bisa disebut kalo irisan himpunan A dan B bisa ditulis dengan (A∩B) = {3,4,5}.

• Gabungan

Gabungan himpunan A dan B (ditulis A ∪ B) yaitu suatu himpunan, dimana anggotanya adalah himpunan A atau anggota himpunan B atau anggota dari keduaduanya.

Gabungan antara himpunan A dan B disimbolkan dengan A ∪ B = {x | x ∈ A atau x ∈ B}

Contohnya:

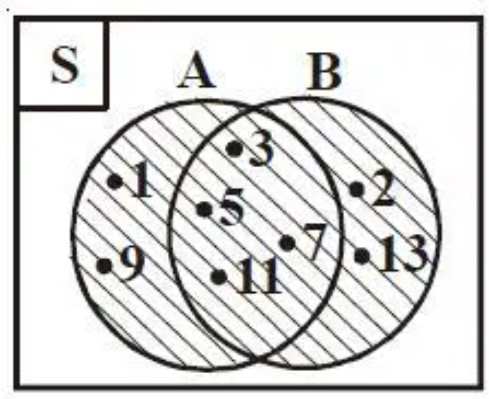
Himpunan A = {1,3,5,7,9,11} dan B= {2,3,5,7,11,13}.

Apabila diantara himpunan A dan himpunan B digabungkan, maka akan membentuk suatu himpunan baru yang anggotanya bisa di tulis menjadi A ∪ B ={1,2,3,5,7,9,11,13}.

• Komplemen

Komplemen himpunan A (ditulis Ac) yaitu suatu himpunan dimana anggotanya adalah anggota himpunan semesta, tapi bukan anggota himpunan A.

Contoh:

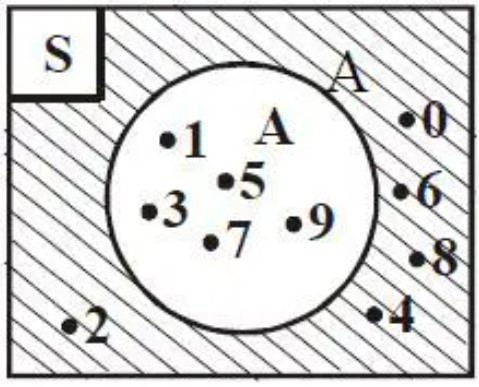
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}.

Coba kamu perhatikan, kalo seluruh anggota S yang bukan dari anggota A membentuk suatu himpunan baru yaitu {0,2,4,6,8}.

Sehingga, komplemen dari himpunan A yaitu Ac = {0,2,4,6,8}.

Contoh Soal Diagram Venn

1. Dari beberapa anak remaja diketahui ada sebanyak 25 orang yang suka minum susu, 20 orang suka minum kopi dan 12 orang lainnya suka susu dan kopi.

Dari data diatas, jawablah pertanyaan yang ada di bawah ini:

a. Jumlah seluruh anak remaja.
b. Jumlah remaja yang suka susu aja.
c. Jumlah remaja yang suka kopi aja.
d. Jumlah remaja yang suka keduanya.

Jawab:

Buat bisa menjawab soal diatas, kamu harus membuat data tersebut kedalam bentuk diagram venn, jadi gambarnya menjadi:

Sehingga diketahui:

a. Jumlah semua anak remaja = 33 orang
b. Jumlah remaja yang suka susu saja = 13 orang
c. Jumlah remaja  yang suka kopi saja = 8 orang
d. Jumlah remaja yang suka keduanya = 12 orang

Semoga materi tentang Diagram Venn Lengkap dengan Gambar bermanfaat untuk teman-teman semua.

Jangan lupa untuk selalu kunjungi Cerdika.com yak! Selamat belajar 😀