Dalam pelajaran matematika, pastinya kita sering sekali mendengarkan atau mengerjakan diagram lingkaran.
Beberapa orang merasa kesulitan untuk bekerja dengan diagram lingkaran ini.
Tapi, kalo kamu mengetahui cara menggunakan rumusnya, maka kamu tidak ada kesulitan dalam menggunakannya.
Ingin tahu, cara menggunakan rumus diagram lingkaran? Yuk, langsung simak ulasannya berikut ini!
Pengertian Diagram Lingkaran
Diagram memliki tipe yang berbeda-beda, misalnya seperti diagram batang, diagram garis, dan diagram lingkaran.
Diagram lingkaran yaitu diagram yang menunjukkan data atau hasil angka-angka dalam bentuk lingkaran.
Biasanya, diagram lingkaran pada soal Matematika sering digunakan buat mengetahui perbandingan dari Total Jumlah yang sesuai dengan pembahasannya.
Dan, dalam diagram batang juga digunakan buat menggambarkan sebuah Presentase Data, Menentukan Statistik, dan lainnya sesuai dengan pembahasan yang dilakukan.
Buat mengetahui Pembesaran Daerah atau Pembatasan Daerah yang berada pada diagram lingkaran ini, dalam pembahasan suatu data.
Tergantung dengan Jumlah Data dan Masing-Masing Data yang menjadi pembahasannya.
Baca juga : Diagram Garis
Rumus Diagram Lingkaran

1. Rumus Diagram Normal
Buat diagram lingkaran normal (dalam bentuk angka), kamu bisa menghitungnya sesuai dengan rumus umum buat diagram biasa tersebut:
A. Rumus Diagram Normal:
Data yang ditanyakan = total data – data yang diketahui secara total
B. Contoh Soal Diagram Normal:
Suatu kelas memiliki total 42 siswa dalam bentuk diagram lingkaran, yaitu sebagai berikut ini:
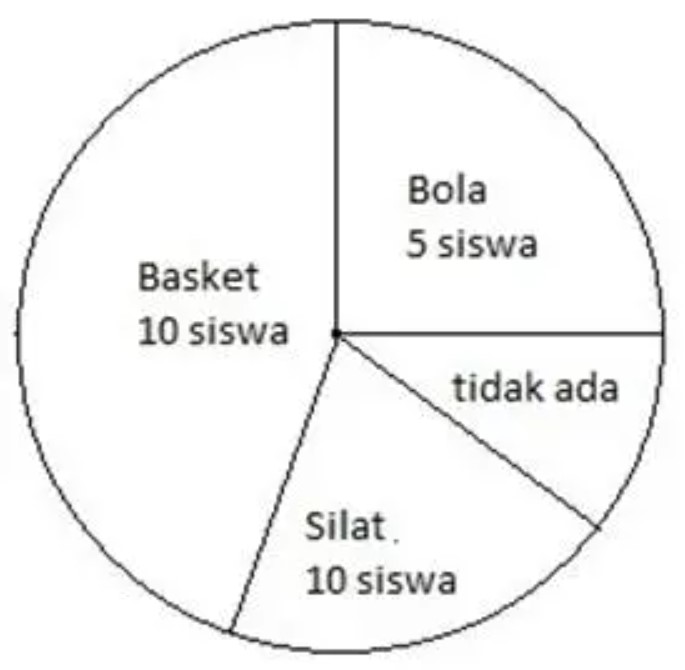
Saat banyak siswa berpartisipasi dalam kegiatan ekstrakurikuler, seperti yang ditunjukkan pada diagram lingkaran diatas. Berapa banyak siswa yang tidak melakukan kegiatan ekstrakurikuler?
Jawab:
Diketahui:
- Total siswa = 42 siswa
- Ekskul basket = 10 siswa
- Ekskul bola = 5 siswa
- Ekskul silat = 10 siswa
Ditanya:
- Siswa yang tidak menghadiri studi ekstrakurikuler?
Dijawab:
Data yang ditanyakan = total data – data yang diketahui secara total
Siswa yang tidak mengikuti pelatihan ekstrakurikuler
- = jumlah total siswa – (ekskul basket + ekskul bola + ekskul silat)
- = 42 siswa – (10 siswa + 5 siswa + 10 siswa)
- = 42 siswa – 25 siswa
- = 17 siswa
Dengan begitu, siswa yang tidak mengikuti ekstrakurikuler yaitu sekitar 17 siswa.
2. Rumus Diagram dalam Derajat
Buat rumus diagram lingkaran, kamu perlu mengetahui angka yang diperlukan.
Yang pertama adalah mengetahui jumlah derajat dan kemudian membaginya dengan 360 derajat.
A. Rumusnya Diagram dalam Derajat:
Nilai yang diperlukan = (nilai sudut/360 °) x nilai total
B. Contoh Soal Diagram dalam Derajat:
Sebuah sekolah memiliki 1.260 siswa. Di sekolah ini, siswa harus menghadiri kegiatan ekstrakurikuler. Saat siswa mengambil program ekstrakurikuler dibentuk menjadi diagram lingkaran dalam bentuk derajat (°) sebagai berikut ini:

Berapa banyak siswa yang mengikuti ekskul musik?
Jawab:
Diketahui:
- Total siswa = 1260 siswa
- Ekskul basket = 130°
- Ekskul bola = 100°
- Ekskul silat = 80°
Ditanya:
- Banyak siswa yang memilih ekskul musik ekstrakurikuler?
Dijawab:
Pertama, cari tahu berapa banyak siswa yang melakukan musik ekstrakurikuler.
- Ekskul musik = 360 ° – (Ekskul basket + ekskul bola + ekskul silat)
- = 360° – (130° – 100° – 80°)
- = 360° – 310°
- = 50°
Kemudian, gunakan rumus buat menentukan jumlah siswa yang belajar musik:
- Jumlah siswa yang memilih musik = (musik/360°) x jumlah total siswa
- = (50°/360°) x 1260 siswa
- = 63000/360
- = 175 siswa
Jadi, ada 175 siswa yang melakukan musik ekstrakurikuler.
3. Rumus Diagram dalam Persentase
Diagram dalam bentuk persentase (%) merupakan hal yang biasa.
Saat ditanya jumlah digit, pertama cari persentase data itu, lalu kalikan dengan jumlah total digit, dan bagi dengan 100%.
A. Rumus Diagram dalam Persentase:
Nilai yang ditanyakan = (nilai persentase/100%) x nilai total
B. Contoh Soal Diagram dalam Persentase:
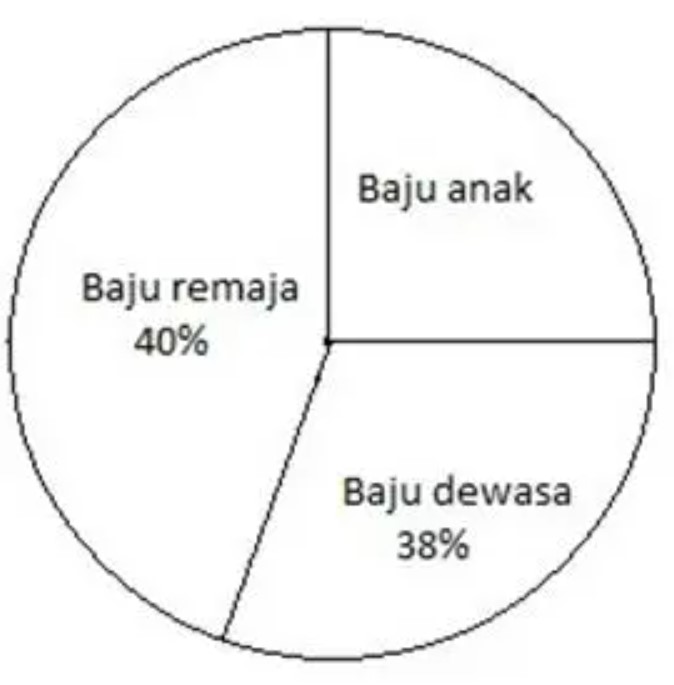
Diketahui dari data diatas, bahwa total barang dagangan yang dijual oleh pedagang yaitu 300.
Mencari berapa banyak item pakaian untuk anak-anak yang dijual oleh penjual pakaian?
Jawab:
Diketahui:
- Total pakaian = 300 bagian
- Pakaian remaja = 40%
- Pakaian dewasa = 38%
Ditanya:
- Berapa banyak baju anak yang dijual?
Dijawab:
Pertama, lihat persentase pakaian anak-anak yang dijual.
- Persentase pakaian anak = 100% – (pakaian remaja + pakaian dewasa)
- = 100% – (40% + 38%)
- = 100% – 78%
- = 22%
Jadi, gunakan persentase pakaian anak yang kamu dapatkan dalam rumus diatas.
- Jumlah pakaian anak = (persentase anak / 100%) x pakaian keseluruhan
- = (22% / 100%) × 300 buah
- = 6600/100
- = 66 buah
Jumlah pakaian anak-anak yang dijual oleh pedagang adalah 66 buah.
4. Rumus Teori Perbandingan
Dalam teori perbandingan ini, bisa digunakan dalam diagram ini kedalam derajat dan persen.
Teori perbandingan sangat berguna buat menemukan nilai dalam penelitian saat sedikit data yang diketahui. Perhatikan penjelasan berikut ini:
Misalnya, diketahui A dan B:
- Persentase A = nilai A atau derajat A = nilai A
- Persentase B = nilai B atau derajat B = nilai B
Dari data diatas, kamu bisa membandingkan A dengan B seperti dibawah ini:
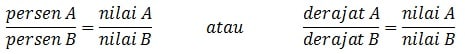
A. Rumus Teori Perbandingan:
Rumus untuk mencari nilai:
Nilai A = (persentase A / persentase B) x nilai B
Atau,
Nilai A = (Derajat A / Derajat B) x Nilai B
Nilai B = (persentase B / persentase A) x nilai AAtau,
Nilai B = (derajat B / derajat A) x Nilai A
Sedangkan,
Rumus untuk mencari persentase atau derajat:
Persentase A = (nilai A / nilai B) x persentase B
Atau
Derajat A = (Nilai A / Nilai B) x Kelas B
Persentase B = (nilai B / nilai A) x persentase AAtau
Derajat B = (nilai B / nilai A) x catatan A
B. Contoh Soal Teori Perbandingan:
Sebuah sekolah memiliki data tentang siswa yang melakukan kegiatan di luar sekolah dalam bentuk diagram lingkaran:
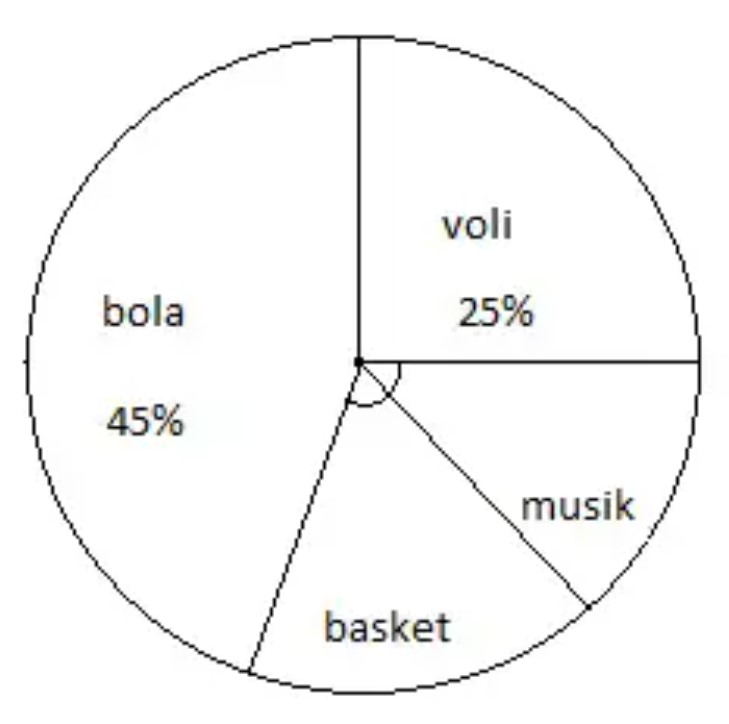
Kalo ada 450 siswa yang mengambil bola, berapa banyak siswa yang bermain bola voli?
Jawab:
Diketahui:
- Persentase bola ekstrakurikuler = 45%
- persen bola voli = 25%
- Jumlah bola = 450 siswa
Ditanya:
- Jumlah siswa yang bermain bola voli?
Dijawab:
- Bola voli = (persentase bola voli / persentase bola voli) x jumlah ekskul bola
- = (25% / 45%) × 450
- = 11250/45
- = 250 siswa
Dengan begitu, jumlah siswa bola voli adalah 250 siswa.
Semoga materi tentang Diagram Lingkaran Lengkap dengan Gambar bermanfaat untuk teman-teman semua.
Jangan lupa untuk selalu kunjungi Cerdika.com yak! Selamat belajar 😀