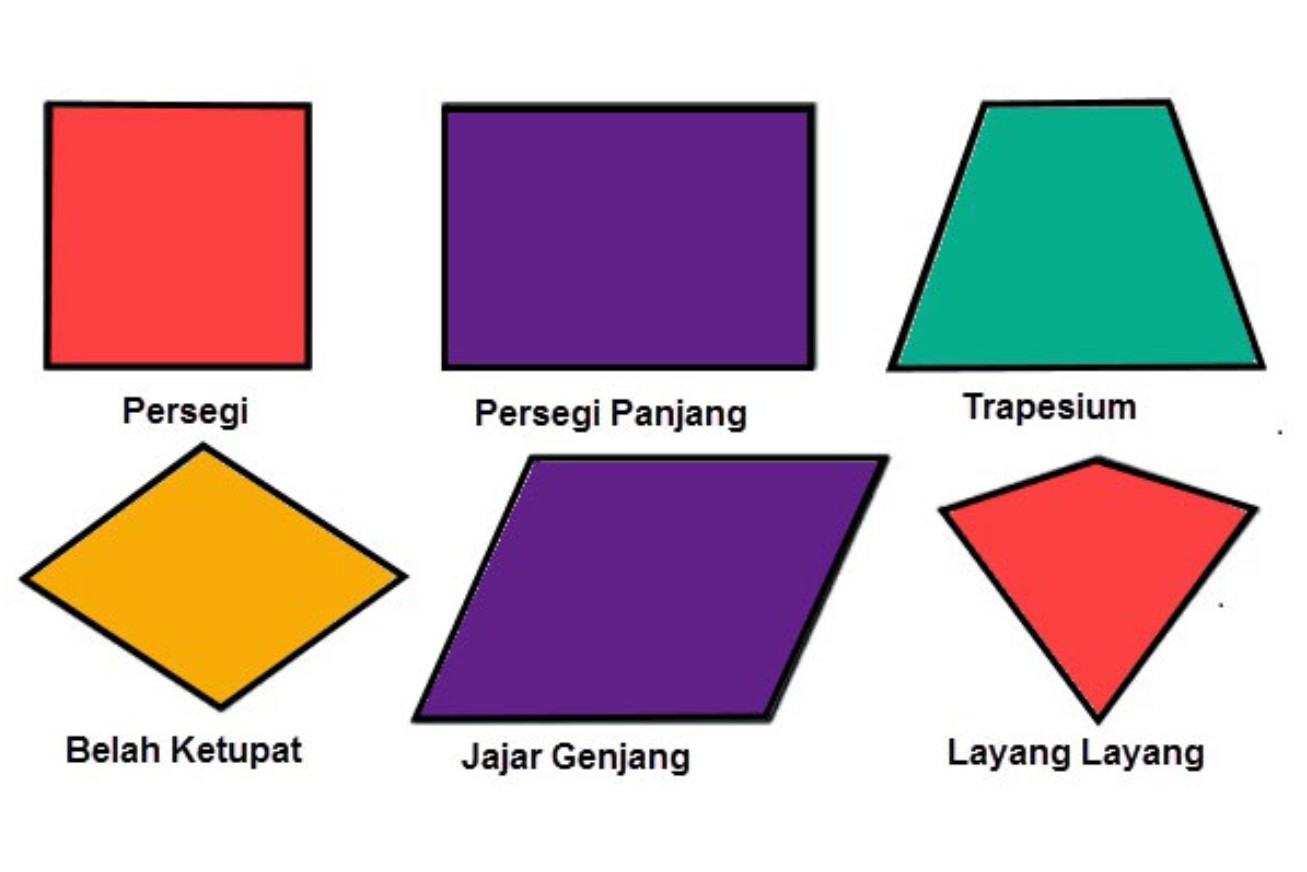
Bangun datar adalah suatu bangun dari bidang datar yang dibatasi oleh garis-garis lurus atau lengkung.

Bangun datar terdiri dari lingkaran, belah ketupat, layang-layang, trapesium, jajar genjang, segitiga, persegi panjang, dan persegi.

Setiap bangun tersebut, memiliki rumus untuk menghitung luas sekaligus keliling yang berbeda satu bangun dengan bangun yang lainnya.

Macam-Macam Bangun Datar

Ada banyak sekali macam/jenis dari sebuah bangun datar, diantaranya sebagai berikut ini:

1. Persegi

Persegi yaitu suatu bangun datar 2 dimensi, yang terbentuk oleh 4 buah rusuk dengan memiliki ukuran sama panjang dan memiliki 4 buah sudut siku-siku.

Persegi juga bisa disebut sebagai bangun datar yang memiliki sisi-sisi sama panjang dan sudut-sudut sama besar.

Sifat Bangun Persegi

• Seluruh sisi-sisinya memiliki ukuran sama panjang dan seluruh sisinya berhadapan sejajar.
• Masing-masing sudut yang dimiliki persegi adalah sudut siku-siku.
• Memiliki 2 diagonal dengan ukuran panjang yang sama dan berpotongan di tengah-tengah serta membentuk sudut siku-siku.
• Masing-masing sudutnya di bagi 2 sama besarnya oleh diagonalnya.
• Mempunyai 4 buah sumbu simetri.

Rumus pada Persegi

• Rumus luas persegi:

L = S x S

• Rumus keliling persegi:

K = S + S + S atau K = 4 x S

Keterangan:

• L = Luas persegi
• K = Keliling persegi
• S = Sisi persegi

2. Persegi Panjang

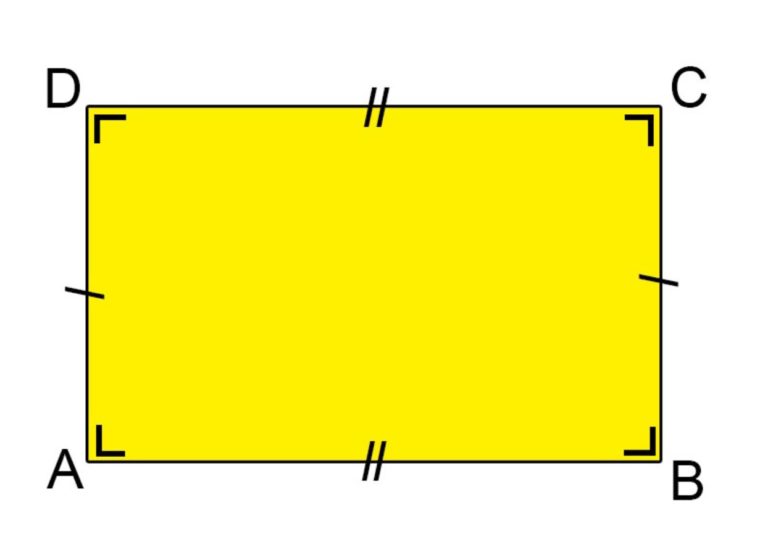
Persegi panjang yaitu suatu bangun datar 2 dimensi, yang terbentuk oleh 2 buah pasang rusuk yang panjang dan sejajar dan memiliki 4 buah sudut siku-siku.

Sifat Bagun Persegi Panjang

• Masing-masing sisi-sisi yang berhadapan memiliki ukuran sama panjang dan sejajar.
• Seluruh sudutnya merupakan sudut siku-siku.
• Memiliki 2 buah diagonal yang sama panjang dan saling berpotongan di titik pusat bangun persegi panjang. Titik itu membagi 2 bagian diagonal dengan ukuran sama panjang.
• Mempunyai 2 buah sumbu simetri yaitu sumbu vertikal dan sumbu horizontal.

Rumus pada Persegi Panjang

• Rumus luas persegi panjang:

L = p x l

• Rumus keliling persegi panjang:

K = 2 x (p + l)

Keterangan:

• L = Luas persegi panjang
• K = Keliling persegi panjang
• p = panjang
• l = lebar

3. Segitiga

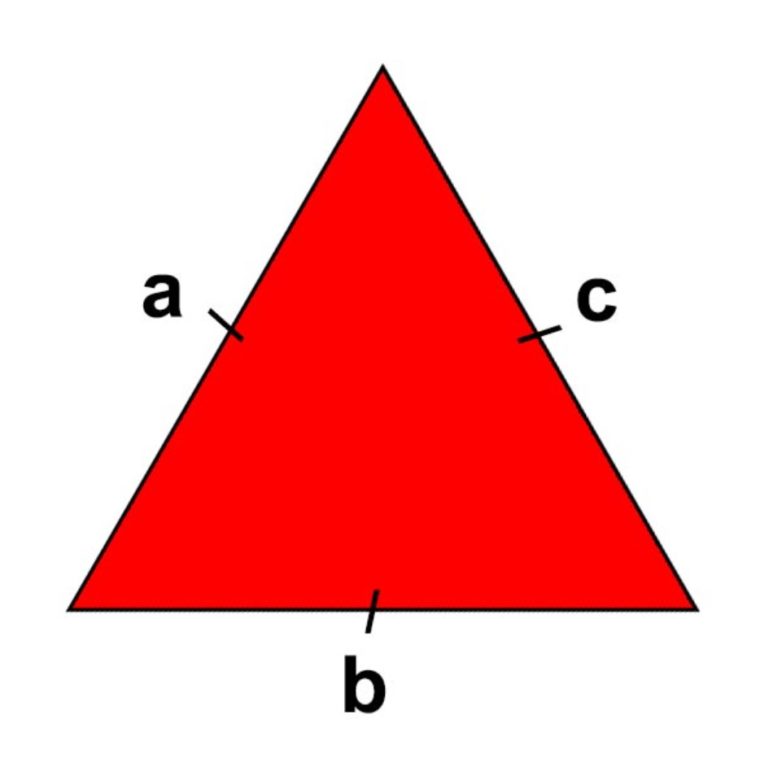
Segitiga adalah suatu bangun datar 2 dimensi, yang dibentuk oleh 3 buah sisi yang berwujud garis lurus dan 3 buah sudut.

Jadi, bangun datar yang terbentuk dari 3 atau lebih garis lurus disebut sebagai “Segitiga”.

Sifat Bangun Segitiga

• Bangun segitiga, ketiga sudutnya memiliki besaran 180º. (kalo dijumlahkan hasilnya 180)
• Sifat Segitiga mempunyai 3 sisi dan juga 3 titik sudut.

Rumus pada Segitiga

• Rumus Luas Segitiga:

Luas = 1/2 x a x t

• Rumus Keliling Segitiga:

Keliling = s + s + s atau K = a + b + c

4. Jajar Genjang

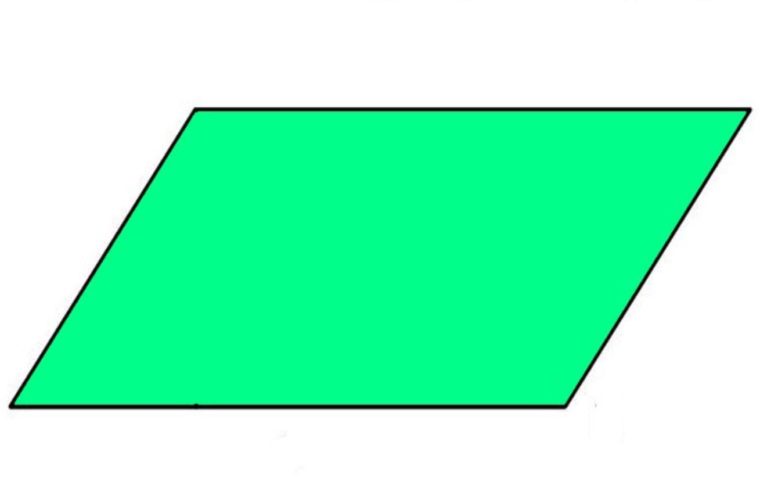
Jajar genjang yaitu suatu bangun datar 2 dimensi, yang dibentuk atas 2 buah pasang rusuk yang dimana pada masing-masingnya memiliki ukuran sama panjang dan sejajar dengan pasangannya.

Lalu, jajar genjang memiliki 2 buah pasang sudut siku-siku yang dimana pada masing-masing sudutnya sama besar dengan sudut depannya.

Sifat Bangun Jajar Genjang

• Jajar genjang tidak mempunyai simetri lipat.
• Jajar genjang memiliki simetri putar tingkat dua.
• Sudut jajar genjang yang berhadapan memiliki ukuran yang sama besar.
• Jajar genjang mempunyai 4 sisi dan 4 sisi sudut.
• Diagonal yang dimilikinya mempunyai panjang yang tidak sama.
• Jajar genjang mempunyai 2 pasang sisi yang sejajar dan sama panjang.
• Jajar genjang mempunyai 2 buah sudut tumpul dan 2 buah sudut lancip.

Rumus pada Jajar Genjang

Keliling (K) : K = 2 x (a + b)

Luas (L) : L =  a x t

Sisi Alas (a) : a = (K / 2) – b

Sisi-Sisi Miring (b) : b = (K / 2) – a

t diketahui L : t = L / a

a diketahui L : a = L / t

5. Trapesium

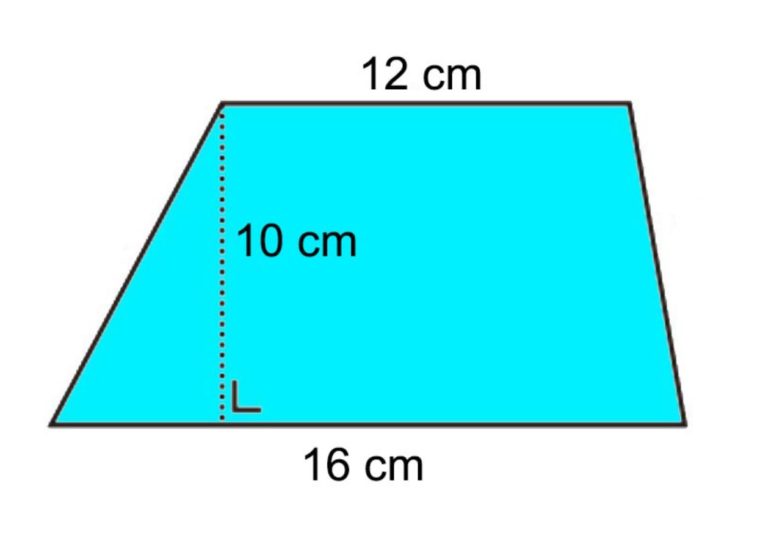
Trapesium yaitu suatu bangun datar 2 dimensi yang dibentuk dari 4 buah rusuk yang 2 buah diantaranya merupakan saling sejajar, tapi panjangnya tidak sama.

Tapi, ada juga trapesium yang rusuk ketiganya merupakan tegak lurus pada rusuk-rusuk sejajarnya yang biasa dikenal dengan sebutan trapesium siku-siku.

Sifat Bangun Trapesium

• Trapesium merupakan bangun datar dengan 4 buah sisi (quadrilateral).
• Mempunyai 2 sisi sejajar yang tidak sama panjang.
• Mempunyai 4 buah titik sudut.
• Minimal pada bangun datar trapesium memiliki 1 titik sudut tumpul.
• Trapesium mempunyai 1 simetri putar.

Rumus pada Trapesium

Nama	Rumus
Luas (L)
Keliling (Kll)	Kll = AB + BC + CD + DA
Tinggi (t)
Sisi a (CD)	atau CD = Kll – AB – BC – AD
Sisi b (AB)	atau AB = Kll – CD – BC – AD
Sisi AD	AD = Kll – CD – BC – AB
Sisi BC	BC = Kll – CD – AD – AB

6. Layang-Layang

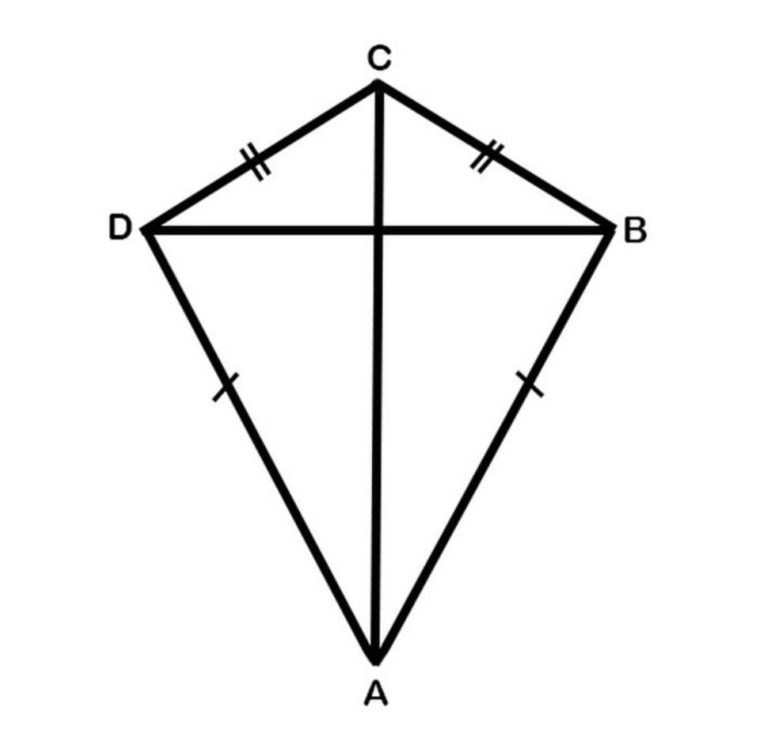
Layang-layang adalah suatu bangun datar 2 dimensi, yang di bentuk oleh 2 buah segitiga sama kaki dan berbentuk segiempat, dimana memiliki alas yang berhimpitan dan berbentuk menjadi suatu layang-layang.

Sifat Bangun Layang-Layang

• Layang-layang merupakan suatu bangun datar dengan 4 sisi (quadrilateral).
• Memiliki 2 pasangan sisi yang membentuk sudut yang berbeda:
  Pasangan 1 : Merupakan sisi a dan sisi b, membentuk sudut ∠ABC.
  Pasangan 2 : Merupakan sisi c dan sisi d, membentuk sudut ∠ADC.
• Memiliki sepasang sudut yang saling berhadapan dengan besar ukuran yang sama:
  Sudut ∠BAD dan ∠BCD saling berhadapan dan memiliki besar yang sama.
• Mempunyai 2 diagonal dengan panjang yang berbeda.
• Diagonal layang-layang saling tegak lurus (90º).
• Diagonal terpanjang merupakan sumbu simetri layang-layang.
• Layang-layang cuma mempunyai 1 sumbu simetri.

Rumus pada Layang-Layang

Luas (L) : L = 1/2 x d1 x d2

Keliling (K) : K = a + b + c + d atau K = 2 x (a + c)

Diagonal 1 (d1) : d1 = 2 x L / d2

Diagonal 2 (d2) : d2 = 2 x L / d1

a atau b : a = (1/2 x K) – c

c atau d : c = (1/2 x K) – a

7. Belah Ketupat

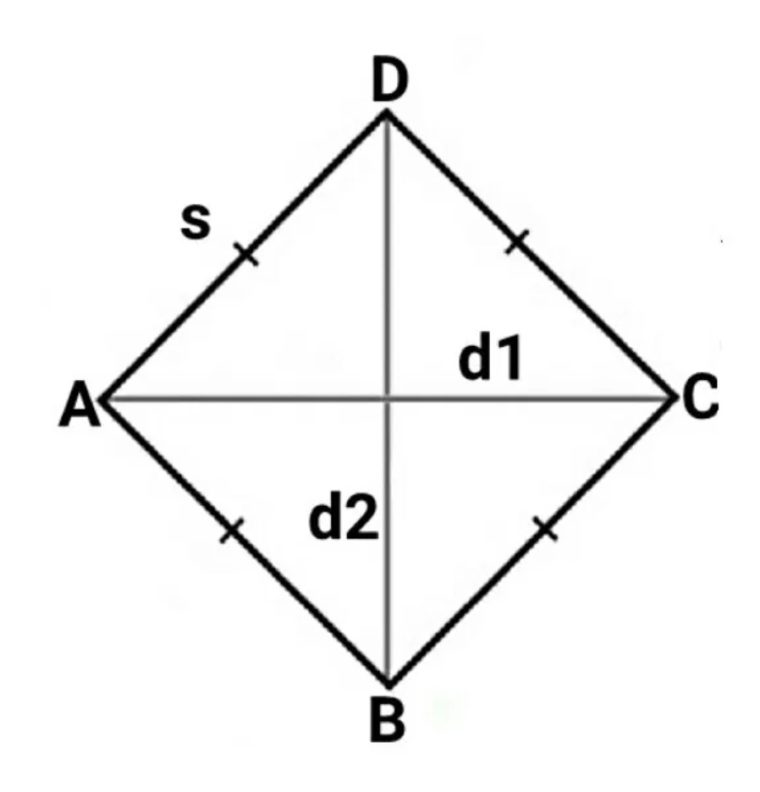
Belah ketupat yaitu suatu bangun datar 2 dimensi, yang dibentuk oleh 4 buah sisi dengan ukuran sama panjang dan memiliki 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan memiliki besar yang sama.

Sifat Bangun Belah Ketupat

• Keempat sisinya sama panjang.
• Memiliki 2 diagonal yang saling tegak lurus:
  Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat, saling tegak lurus membentuk sudut siku-siku (90°).
• Sudut yang saling berhadapan memiliki besar yang sama.
• Besar pada keempat titik sudutnya adalah 360º.
• Mempunyai 2 sumbu simetri yang dimana adalah diagonalnya.
• Belah ketupat mempunyai simetri putar tingkat 2.
• Mempunyai 4 buah sisi dan 4 buah titi sudut.
• Keempat sisi belah ketupat memiliki panjang yang sama.

Rumus pada Belah Ketupat

Keliling (K) : K = s + s + s + s atau K = s x 4

Luas (L) : L = 1/2 x d1 x d2

Sisi (s) : s = K / 4

Diagonal 1 (d1) : d1 = 2 x L / d2

Diagonal 2 (d2) : d2 = 2 x L / d1

8. Lingkaran

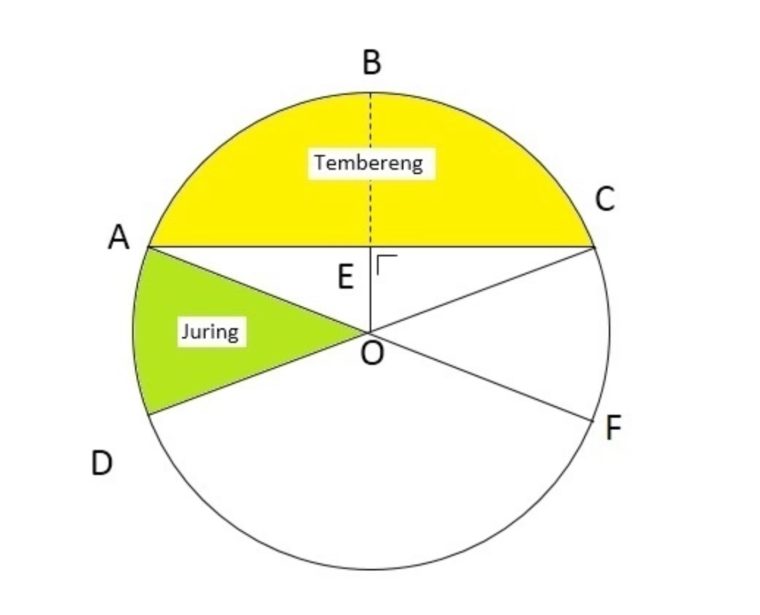
Lingkaran adalah bangun datar 2 dimensi, yang dibentuk oleh himpunan semua titik yang mempunyai jarak sama dari suatu titik tetap.

• Pusat lingkaran (P) : Yaitu titik tetap pada lingkaran disebut sebagai pusat lingkaran.
• Jari-jari (r) : Yaitu jarak titik lainnya pada pusat lingkaran disebut sebagai jari-jari lingkaran.
• Garis lengkung : Yaitu himpunan seluruh titik lingkaran, lalu membentuk garis lengkung yang menjadi keliling lingkaran.
• Diameter (d) : Yaitu garis yang ditarik dari 2 titik pada garis lengkung dan melewati titik pusat. Diameter lingkaran memiliki panjang 2 x r.
• phi (π): Yaitu nilai perbandingan antara keliling dan juga diameter lingkaran selalu konstan adalah 3,14 atau 22/7.

Sifat Bangun Lingkaran

• Mempunyai simetri putar tak terhingga.
• Memiliki simetri lipat dan juga sumbunya yang tak terhingga.
• Tidak mempunyai titik sudut.
• Mempunyai satu buah sisi.

Rumus pada Lingkaran

Diameter (d) : d = 2 x r

Jari-jari (r) : r = d /2

Luas (L) : L = π x r x r atau L = π x r²

Keliling (K) : K = π x d

Mencari r : r = K / 2π atau r = √L / √π

Contoh Soal Bangun Datar

1. Suatu bangun persegi panjang, mempunyai p = 10 cm dan l = 5 cm, terdiri atas EFGH. Coba hitunglah:

• Hitunglah luas persegi panjang EFGH!
• Hitunglah keliling persegi panjang EFGH!

Jawab:

Diketahui:

• p = 10 cm
• l = 5 cm

Ditanya:

• Hitunglah luas persegi panjang EFGH!
• Hitunglah keliling persegi panjang EFGH!

Dijawab:

a. Rumus luas persegi panjang EFGH

• L= p x l
• L  = 10 cm x 5 cm
• L = 50 cm²

Jadi, luas persegi panjang EFGH tersebut adalah 50 cm².

b. Rumus Keliling sama persegi panjang EFGH

• 2 x (p + l)
• = 2 x (10 cm + 5 cm)
• = 2 x 15 cm
• = 30 cm

Jadi, keliling persegi panjang EFGH tersebut adalah 50 cm.

2. Apabila diketahui suatu lingkaran memiliki diameter 14 cm. Maka, berapakah luas lingkaran tersebut?

Jawab:

Diketahui:

• d = 14 cm

Sebab d = 2 × r, maka:
r = d/2
r = 14/2
r = 7 cm

Ditanya:

• Luas lingkaran …?

Dijawab:

• Luas = π × r²
• Luas = 22/7 × 7²
• Luas = 154 cm²

Sehingga, luas lingkaran tersebut adalah 154 cm².

Terima kasih teman-teman sudah membaca tentang Macam-Macam Bangun Datar diatas tadi.

Semoga bisa membantu dan bermanfaat. Jangan lupa juga untuk selalu kunjungi cerdika.com yak 😀