Trapesium yaitu suatu bangun datar yang terdiri dari 2 buah sisi sejajar yang panjangnya tidak sama dan 2 sisi lainnya.
Trapesium juga memiliki nama yang lain loh, yaitu “Trapezoid”.
Dalam kesempatan kali ini, kita akan mempelajari pengertian dan rumus-rumus trapesium beserta contoh soalnya.
Yuk, langsung aja simak pembahasannya berikut dibawah ini!
Sifat Trapesium
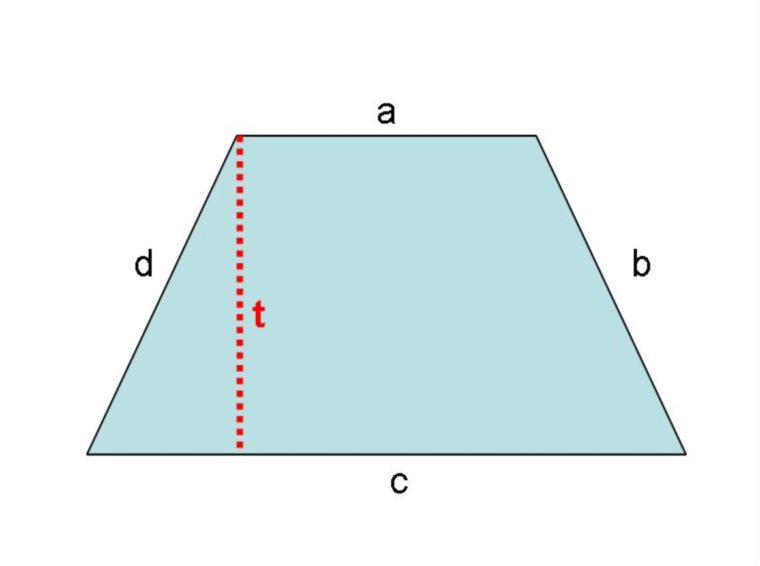
Berdasarkan jenis-jenisnya, trapesium memiliki beberapa sifat-sifat seperti dibawah ini:
- Trapesium memiliki 4 buah sudut dan jumlah 2 sudut yang berdekatan (sudut dalam sepihak) yaitu 180°.
- Trapesium memiliki sepasang sisi yang sejajar.
- Untuk trapesium sama kaki memiliki panjang diagonal sama, ukuran sudut-sudut alasnya sama, dan bisa menempati bingkainya dengan dua cara.
- Untuk trapesium siku-siku mempunyai 2 sudut siku-siku.
- Untuk trapesium sebarang memiliki panjang kaki yang tidak sama, kaki-kakinya juga tidak ada yang tegak lurus ke sisi sejajarnya, dan besar keempat sudutnya berbeda-beda.
- Minimal memiliki 1 titik sudut tumpul.
- Mempunyai 1 simetri putar.
Jenis-Jenis Trapesium
Trapesium ini terbagi menjadi beberapa jenis, diantaranya sebagai berikut ini:
1. Trapesium Sama Kaki
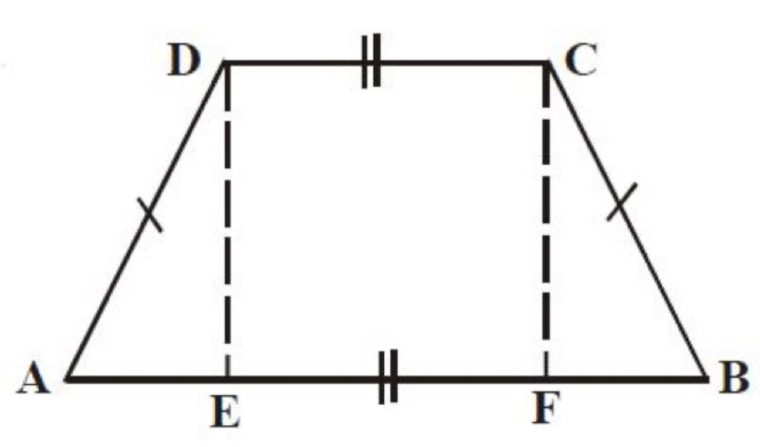
Trapesium sama kaki merupakan trapesium yang mempunyai sepasang sisi yang sama panjang.
Jenis Trapesium sama kaki ini, memiliki 1 simetri lipat dan juga 1 simetri putar.
2. Trapesium Siku-Siku
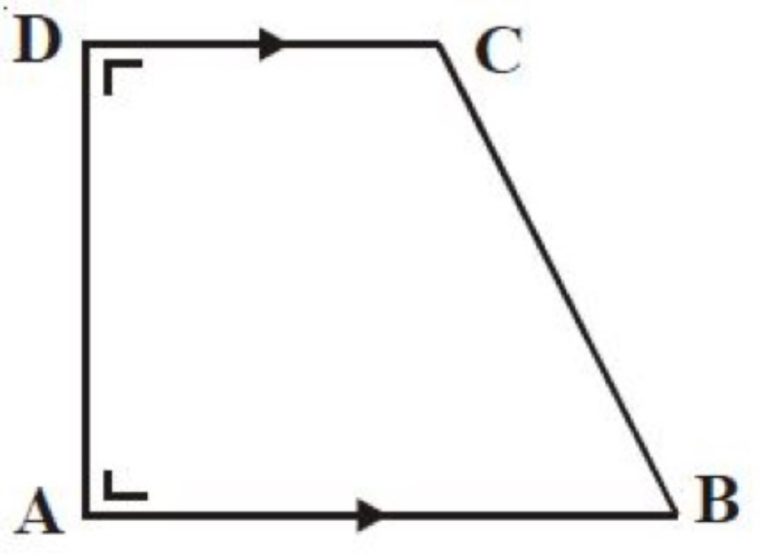
Trapesium siku-siku merupakan jenis trapesium yang mempunyai 2 sudut siku-siku.
Jenis trapesium siku-siku ini, tidak memiliki simetri lipat dan cuma memiliki 1 simetri putar.
3. Trapesium Sembarang
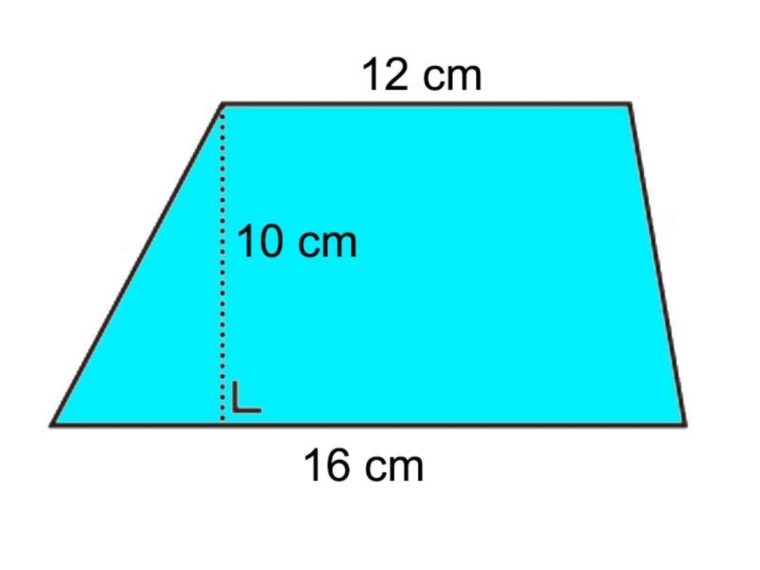
Trapesium sembarang adalah sebuah trapesium yang keempat sisinya tidak sama panjang dan tidak memiliki sudut siku-siku.
Jenis trapesium sembarang ini, tidak memiliki simetri lipat dan cuma memiliki 1 simetri putar.
Rumus Trapesium
1. Rumus Luas Trapesium
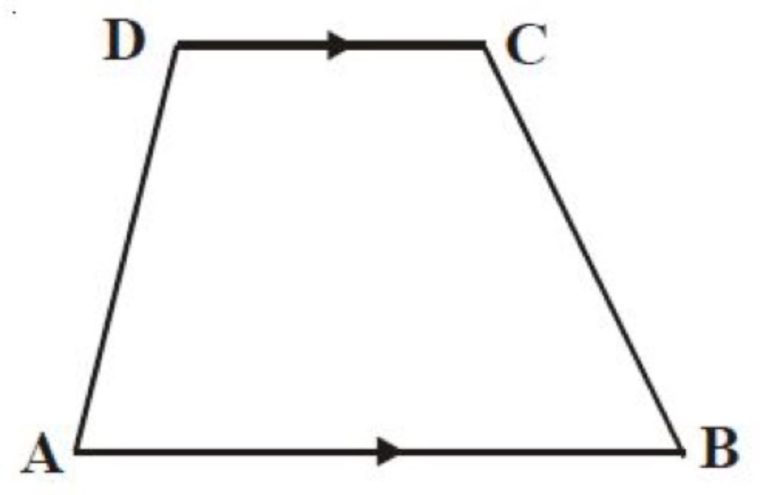
Coba perhatikan gambar diatas, ada dua buah segitiga, yaitu segitiga ABC dan segitiga ACD. Buat menentukan luas trapesium tersebut, dapat dengan menentukan luas kedua segitiga.
Rumusnya:
Luas trapesium ABCD = Luas segitiga ABC + Luas segitiga ACD
Luas trapesium ABCD = ((1/2) x b x t) + ((1/2) x a x t)
L = (1/2) x t x (b + a)
atau,
L = ((a + b) x t) / 2
Keterangan:
- L = Luaas trapesium
- a dan b = panjang sisi-sisi sejajar trapesium
- t = tinggi trapesium
2. Rumus Keliling Trapesium
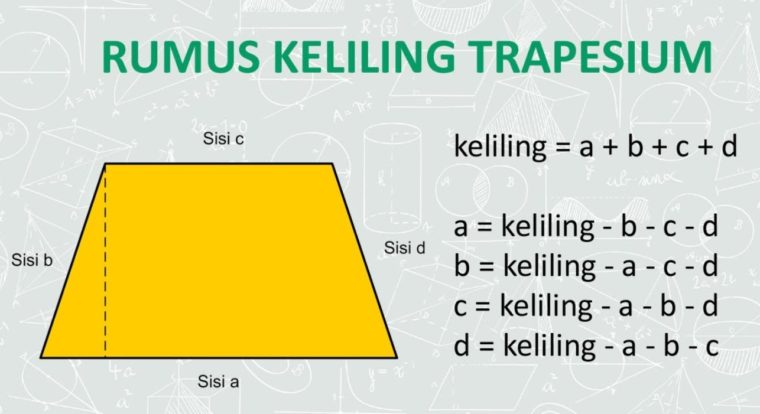
Secara umum, buat menghitung keliling bangun datar bisa dilakukan dengan menghitung jumlah panjang setiap sisinya.
Coba kamu perhatikan gambar trapesium berikut dibawah ini:
Pada gambar tersebut terdapat trapesium ABCD. Keliling trapesium tersebut bisa dihitung dengan:
Keliling = panjang AB + panjang BC + panjang CD + panjang DA
K = a + b + c + d
Keterangan:
- K = Keliling trapesium
- a, b, c, d = panjang masing-masing sisi trapesium
3. Rumus Tinggi Trapesium
(2xt) / (x+y)
Keterangan:
- x = panjang sisi AB
- y = panjang sisi DC
- t = tinggi
4. Rumus Panjang Sisi Trapesium
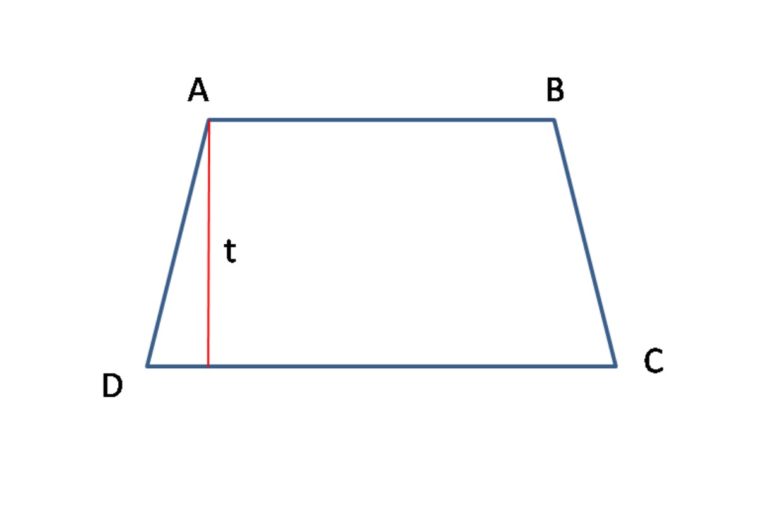
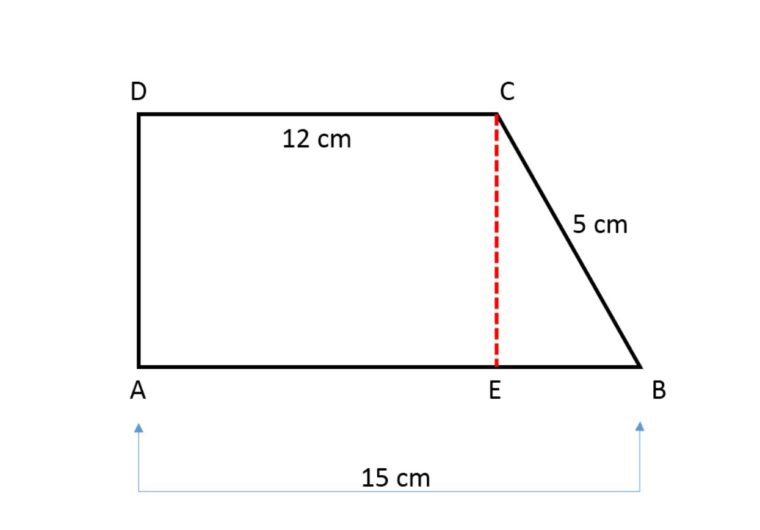
Coba kamu perhatikan contoh gambar dibawah ini:
Mencari sisi a (AB) : a = 2 x L / t – b atau AB = K – CD – BC – AD
Mencari sisi b (CD) : b = 2 x L / t – a atau CD = K – AB – BC – AD
Mencari sisi AD : = AD = K – CD – BC – AB
Mencari sisi BC : BC = K – CD – AD – AB
Keterangan:
- L = Luas trapesium
- t = tinggi trapesium
- K = Keliling trapesium
- a, b adalah sisi yang sejajar, sisi a adalah panjang AB dan sisi b adalah panjang DC.
Contoh Soal Rumus Trapesium

1. Ada sebuah trapesium dengan panjang sisi sejajar masing-masing 20 cm dan 12 cm serta tinggi 6 cm. Berapakah luas trapesium tersebut?
Jawab:
Diketahui:
- sisi sejajar = 20 cm dan 12 cm
- t = 6 cm
Ditanya:
- Luas trapesium …?
Dijawab:
- L = ½ × jumlah panjang sisi sejajar × tinggi
- L = ½ × (20 + 12) × 6
- L = ½ × 32 × 6
- L = 96 cm²
Sehingga, luas trapesium tersebut adalah 96 cm².
2. Diketahui sebuah trapesium memiliki luas 104 cm² dan panjang sisi sejajarnya adalah 15 cm dan 11 cm. Coba, tentukan tinggi trapesium tersebut!
Jawab:
Diketahui:
- a = 15 cm
- b = 11 cm
- L = 104 cm²
Ditanya:
- tinggi trapesium …?
Dijawab:
- t = 2 x L / (a + b)
- t = 2 x 104 / (15+ 11)
- t = 208 / 26
- t = 8 cm²
Sehingga, tinggi dari sebuah trapesium tersebut adalah 8 cm².
3. Sebuah trapesium memiliki sisi sejajar a = 13 cm, b = 8 cm, t = 4 cm dan sisi lainnya c = 5 cm, d = 7 cm. Coba tentukan keliling dari trapesium tersebut!
Jawab:
Diketahui:
- sisi sejajar : a = 13 cm, b = 8 cm, t = 4 cm
- sisi lainnya : c = 5 cm, d = 7 cm
Ditanya:
- Keliling trapesium …?
Dijawab:
- K = a + b + c + d
- K = 13 cm + 8 cm + 5 cm + 7 cm
- K = 33 cm
Sehingga, keliling trapesium tersebut adalah 33 cm.
Gimana pemabahasan diatas? Sangat mudah buat dipahami dan dipelajari kan?
Terima kasih teman-teman sudah membaca tentang Rumus Trapesium diatas tadi.
Semoga bisa membantu dan bermanfaat. Jangan lupa juga untuk selalu kunjungi cerdika.com yak 😀