Dalam pelajaran matematika, Persamaan kuadrat adalah sebuah persamaan dari variabel yang memiliki pangkat tertinggi dua.
Atau,
Persamaan kuadrat adalah persamaan polinomial (suku banyak) yang mempunyai orde (pangkat) dua.
Persamaan kuadarat sering juga disebut sebagai persamaan parabola.
Karena, kalo bentuk persamaan kuadrat digambarkan ke dalam gambar koordinat xy maka akan membentuk grafik parabolik.
Lalu, gimana bentuk dan cara untuk menyelesaikan persamaan kuadrat ini? Simak ulasan selengkapnya di bawah ini ya!
Bentuk Umum Persamaan Kuadrat

y = ax2 + bx + c
Dengan a, b, c ∈ R dan a ≠ 0
Keterangan:
- x merupakan variabel
- a merupakan koefisien kuadrat dari x2
- b merupakan koefisien liner dari x
- c merupakan konstanta
Penyelesaian atau pemecahan dari suatu persamaan ini disebut sebagai akar-akar persamaan kuadrat.
Sedangkan, untuk pengertian dari kuadrat itu sendiri adalah akar kuadrat dari bilangan x sama dengan bilangan r sedemikian.
Jadi r2 = x, atau, di dalam kata lain, bilangan r yang jika kita kuadratkan (hasil kali dengan bilangan itu sendiri) nilainya akan sama dengan x.
Persamaan Kuadrat

Dari uraian di atas, maka bisa kamu ketehui kalo nilai koefisen a, b, dan c yang menentukan bentuk parabola dari fungsi persamaan kuadrat dalam koordinat xy.
Persamaan kuadrat merupakan sebuah persamaan yang pangkat tertinggi dari variabelnya yaitu 2.
Bentuk umum dari persamaan kuadrat ditulis:
ax2 + bx + c = 0, a≠0 dan a,b,c elemen R
Keterangan:
- x adalah variabel dari persamaan kuadrat
- a adalah koefisien x2
- b adalah koefisien x
- c adalah konstanta
Berikut dibawah ini penjelasan selengkapnya:
1. Koefisien a mencari cekung atau cembungnya kurva parabola
Apabila nilai a>0 parabola akan terbuka ke atas, apabila a<0 parabola akan terbuka ke bawah. Perhatikan gambar dibawah ini:

2. Koefisien b mencari posisi x puncak parabola
Koefisen b dalam menentukan posisi x sebagai puncak parabla atau sumbu simetri dari kurva yang terbentuk senilai x = -b/2a. Perhatikan gambar di bawah ini:
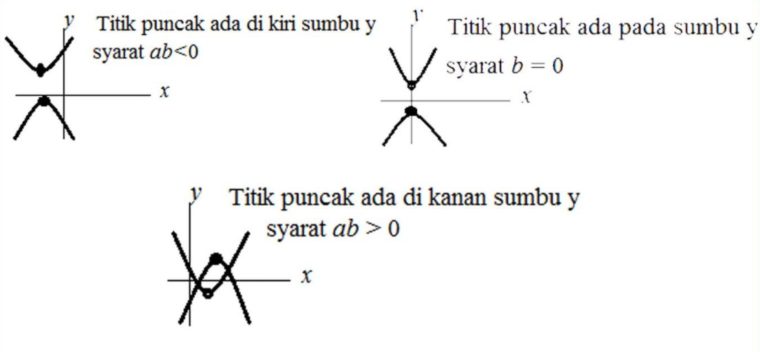
3. Koefisien c mencari titik potong fungsi parabola dengan sumbu y
Perhatikan gambar di bawah ini:
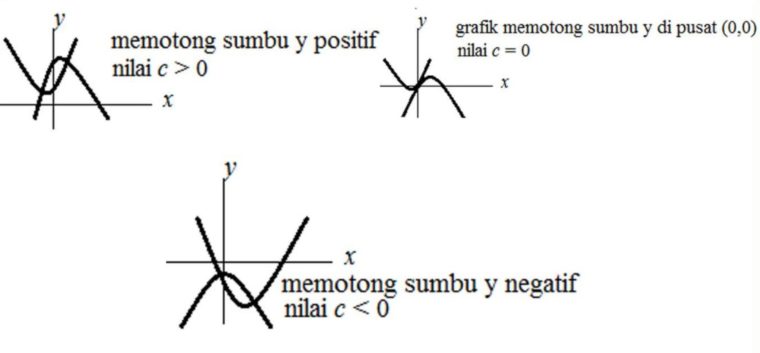
Sifat Akar Persamaan Kuadrat

Akar-akar persamaan kuadrat sangat ditentukan oleh adanya nilai diskriminan (D = b2 – 4ac).
Dimana, hal tersebut yang membedakan jenis akar-akar persamaan kuadrat menjadi 3, diantaranya sebagai berikut ini:
- Apabila D > 0, maka persamaan kuadrat mempunyai dua akar real yang berlainan.
1. Apabila D berbentuk kuadrat sempurna, maka kedua akarnya adalah rasional.
2. Apabila D gak berbentuk kuadrat sempurna, maka kedua akarnya adalah irasional. - Apabila D = 0, maka persamaan kuadratnya memiliki dua akar yang sama (akar kembar), real, dan juga rasional.
- Apabila D < O, maka persamaan kuadratnya gak memiliki akar real atau kedua akarnya gak real (imajiner).
Bentuk dari perluasan untuk akar-akar real, diantaranya sebagai berikut ini:
1. Kedua Akar Positif
Kedua akarnya positif apabila:
- D ≥ 0
x1 + x2 > 0
x1 x2 > 0
2. Kedua Akar Negatif
Kedua akarnya negatif apabila:
- D ≥ 0
x1 + x2 < 0
x1 x2 > 0
3. Kedua Akar Berlainan Tanda
Kedua akar berlainan tanda apabila:
- D > 0
x1 x2 < 0
4. Kedua Akar Bertanda Sama
Kedua akar bertanda sama apabila:
- D ≥ 0
x1 x2 > 0
5. Kedua Akar Saling Berlawanan
Kedua akar saling berlawanan apabila:
- D > 0
x1 + x2 = 0 (b = 0)
x1 x2 < 0
6. Kedua Akar Saling Berkebalikan
Kedua akar saling berkebalikan apabila:
- D > 0
x1 + x2 = 1 (c = a)
Jenis-Jenis Akar Persamaan Kuadrat

Untuk mengetahui berbagai macam dari akar persamaan kuadrat, kita juga bisa mengetahuinya dengan memakai rumus D = b2 – 4ac.
Apabila terbentuk nilai D, maka kamu akan dengan mudah dapat menemukan berbagai akarnya.
Berikut ini, ada beberapa jenis dari persamaan kuadrat secara umum, diantaranya yaitu:
1. Akar Real (D ≥ 0)
Akar real berlainan jika diketahui = D > 0
Contohnya:
Tentukan jenis akar dari persamaan di bawah ini:
- x2 + 4x + 2 = 0 !
Jawab:
Dari persamaan = x2 + 4x + 2 = 0, maka dapat kamu ketahui:
Diketahui:
- a = 1
- b = 4
- c = 2
Penyelesaian:
- D = b2 – 4ac
- D = 42 – 4(1)(2)
- D = 16 – 8
- D = 8 (D>8, maka akarnya pun adalah akar real tapi berbeda)
Akar real sama x1 = x2 jika diketahui D = 0
2. Akar Imajiner/Tidak Real (D < 0)
Contohnya:
Tentukanlah jenis akar dari persamaan di bawah ini:
- x2 + 2x + 4 = 0 !
Jawab:
Dari persamaan tersebut yaitu: = x2 + 2x + 4 = 0, maka
Diketahui:
- a = 1
- b = 2
- c = 4
Penyelesaian:
- D = b2 – 4ac
- D = 22 – 4(1)(4)
- D = 4 – 16
- D = -12
(D<0, sehingga akar-akarnya merupakan akar tidak real)
3. Akar Rasional ( D = k2 )
Contohnya:
Tentukan jenis akar dari persamaan di bawah ini:
- x2 + 4x + 3 = 0
Jawab:
Dari persamaan tersebut yaitu: = x2 + 4x + 3 = 0, maka
Diketahui:
- a = 1
- b = 4
- c = 3
Penyelesaian:
- D = b2 – 4ac
- D = 42 – 4(1)(3)
- D = 16 – 12
- D = 4 = 22 = k2
(Karena D=k2=4, sehingga akar persamaannya merupakan akar rasional)
Cara Mencari Akar Persamaan Kuadrat

Ada tiga cara atau metode dalam mencari akar-akar buat menyelesaikan persamaan kuadrat.
Berikut dibawah ini, penjelasan buat masing-masing cara mencari akar-akar persamaan kuadrat.
1. Faktorisasi
Faktorisasi atau pemfaktoran yaitu suat metode atau cara dalam mencari akar-akar persamaan kuadrat dengan mencari nilai yang apabila dikalikan akan menghasilkan nilai lain.
Ada 3 bentuk persamaan kuadrat dengan faktorisasi akar-akar yang berbeda, diantaranya yaitu:
| No | Persamaan Kuadrat | Faktorisasi Akar-akar |
| 1 | x2 + 2xy + y2 = 0 | (x + y)2 = 0 |
| 2 | x2 – 2xy + y2 = 0 | (x – y)2 = 0 |
| 3 | x2 – y2 = 0 | (x + y)(x – y) = 0 |
Untuk lebih memahami uraian di atas, perhatikan contoh soal di bawah ini:
Selesaikan persamaan kuadrat berikut ini, dengan menggunakan metode faktorisasi 5x2+13x+6=0!
Jawab:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x(x + 2) + 3(x + 2) = 0
(5x + 3)(x + 2) = 0
5x = -3
x = -3/5, atau x = -2
Sehingga, himpunan penyelesaian HP = (-3/5, -2)
2. Kuadrat Sempurna
Bentuk kuadrat sempurna merupakan bentuk persamaan kuadrat yang menghasilkan bilangan rasional.
Hasil dari persamaan kuadrat sempurna umumnya menggunakan rumus sebagai berikut:
(x+p)2 = x2 + 2px + p2
Penyelesaian umum dari persamaan kuadarat sempurna, yaitu sebagai berikut ini:
- (x+p)2 = x2 + 2px + p2
Dengan pemisalan (x+p)2 = q , maka:
- (x+p)2 = q
- x+p = ± q
- x = -p ± q
Berikut contoh soal mengenai penggunaan metode persamaan sempurna.
Selesaikan persamaan x2 + 6x + 5 = 0 menggunakan metode persamaan kuadrat sempurna!
Penyelesaian:
- x2 + 6x +5 = 0
- x2 + 6x = -5
Langkah selanjutnya yaitu tambahkan satu angka di ruas kanan dan kiri sampai bisa berubah ke bentuk kuadrat sempurna.
- x2 + 6x + 9 = -5 + 9
- x2 + 6x + 9 = 4
- (x+3)2 = 4
- (x+3) = √4
- x = 3 ± 2
Jadi, hasil akhirnya adalah x = -1 atau x = -5
3. Rumus Kuadrat ABC
Rumus ABC adalah alternatif pilihan saat persamaan kuadrat udah tidak bisa diselesaikan dengan metode faktorisasi atau kuadrat sempurna.
Berikut ini, rumus formula abc pada persamaan kuadrat ax2 + bx + c = 0.
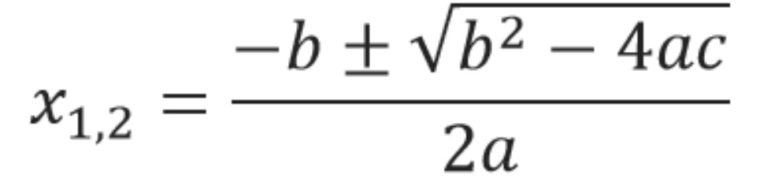
Nah, dibawah adalah contoh penyelesaian soal persamaan kuadrat menggunakan formula/rumus abc.
Coba kamu selesaikan persamaan x2 + 4x – 12 = 0 menggunakan metode formula abc!
Penyelesaian:
x2 + 4x – 12 = 0
dengan a=1, b=4, c=-12
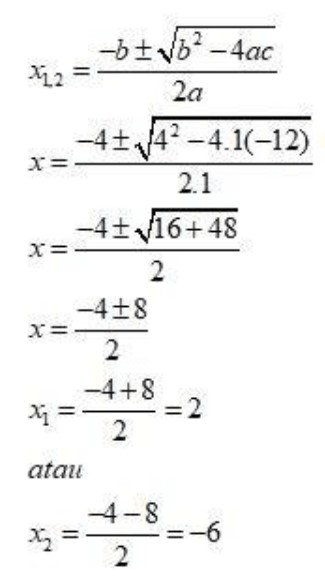
Menyusun Persamaan Kuadrat Baru

Berikut dibawah ini, ada beberapa cara yang bisa digunakan untuk menyusun persamaan kuadrat baru, yaitu:
1. Menyusun persamaan jika telah diketahui akar-akarnya
Kalo sebuah persamaan memiliki akar x1 dan x2, maka persamaan dari akar tersebut bisa dinyatakan dalam bentuk seperti ini:
(x- x1)(x- x2)=0
Contohnya:
Tentukan persamaan kuadrat dimana akar-akarnya diantaranya -2 dan 3.
Penyelesaian:
x1 =-2 dan x2=3
(x-(-2))(x-3)=0
(x+2)(x+3)
x2-3x+2x-6=0
x2-x-6=0Jadi, hasil persamaan dari akar-akar tersebut adalah x2-x-6=0
2. Menyusun Persamaan Kuadrat Jika Jumlah dan Hasil Kali Akar Diketahui
Kalo akar-akar persamaan kuadratnya dengan jumlah dan kali x1 dan x2 udah diketahui, maka persamaan kuadratnya bisa diubah dalam bentuk sebagai berikut ini:
x2-( x1+ x2)x+(x1.x2)=0
Contohnya:
Tentukan persamaan kuadrat yang memiliki akar 3 dan 1/2.
Penyelesaian:
x1=3 dan x2= -1/2
x1+ x2=3 -1/2 =6/2 – 1/2 = 5/2
x1.x2 = 3 (-1/2) = -3/2Sehingga, persamaan kuadratnya yaitu:
x2-( x1+ x2)x+(x1.x2)=0
x2– 5/2 x – 3/2=0 (masing-masing ruas dikali 2)
2x2-5x-3=0Jadi, persamaan kuadratnya dari akar 3 dan 1/2 adalah 2x2-5x-3=0
Contoh Soal Persamaan Kuadrat
Soal 1. Bentuk Umum Persamaan Kuadrat
Apabila bentuk umum dari persamaan x2 – 4 = 3(x – 2) merupakan ax2 + bx + c = 0, maka nilai a, b, dan c berturut-turut adalah ….
A. 1, -3, 2
B. 1, -2, 3
C. 1, 3, -2
D. 1, -3, -10
Jawab:
Untuk menentukan nilai a, b, dan c maka kita harus merubah bentuk soal menjadi bentuk umum terlebih dahulu.
Caranya:
⇒ x2 – 4 = 3(x – 2)
⇒ x2 – 4 = 3x – 6
⇒ x2 – 4 – 3x + 6 = 0
⇒ x2 – 3x + 2 = 0
⇒ a = 1, b = -3, dan c = 2
Jawaban: A
Soal 2. Menentukan Akar Persamaan Kuadrat
Apabila salah satu akar dari persamaan kuadrat x2 + 2x + c = 0 yaitu 3, maka akar lainnya adalah ….
A. x = 5
B. x = 3
C. x = -5
D. x = -15
Jawab:
Langkah pertama yang harus kita lakukan adalah mensubstitusikan nilai x = 3 untuk mengetahui nilai c:
x2 + 2x + c = 0
32 + 2(3) + c = 0
9 + 6 + c = 0
15 + c = 0
c = -15
Langkah kedua yang harus kita lakukan adalah mensubstitusikan nilai c sehingga persamaanya menjadi:
x2 + 2x + c = 0
x2 + 2x – 15 = 0
Kemudian menentukan nilai akarnya dengan pemfaktoran:
(x + 5)(x – 3) = 0
x = -5 atau x = 3
Jawaban: C
Semoga materi tentang Persamaan Kuadrat Lengkap dengan Gambar bermanfaat untuk teman-teman.
Jangan lupa untuk selalu kunjungi Cerdika.com ya! Selamat belajar 😀

