Materi tentang ukuran sudut dan ukuran radian merupakan materi pembelajaran yang diberikan saat duduk dibangku kelas VII Semester Genap.
Ukuran sudut dan ukuran radian digunakan untuk mengukur suatu sudut tentunya.
Materi Matematika yang tergolong ke dalam Trigonometri ini juga dipelajari saat kelas X Semester genap
Pahami juga : Grafik Fungsi Trigonometri
Ukuran Derajat

Ukuran derajat adalah ukuran yang dapat dibentuk pada bidang datar dengan satuan (°) menggambarkan 1/360 dari putaran penuh.
Ada juga suku yang lebih kecil dari pada derajat, yaitu menit (‘) , detik (“) . Hubungan dari kedua ukuran tersebut adalah :
1 derajat = 60 menit atau 1° = 60′
1 menit = 60 detik atau 1′ = 60″
Ukuran Radian

Kita juga mengenal sebutan Ukuran Radian. Ukuran Radian adalah satuan sudut dalam suatu bidang dengan lambang “rad”.
Satu radian atau 1 rad adalah besarnya sudut yang dibentuk oleh dua buah jari-jari lingkaran berjari-jari 1 meter dan membentuk busur sepanjang juga 1 meter. Atau dalam gambar di sebuah ini r = b = 1 meter.
Panjang busur suatu lingkaran dapat dihitung langsung dengan mengalikan besarnya sudut dengan jari-jari lingkaran, apabila besarnya sudut telah dalam satuan radian. Contoh seperti gambar di bawah ini :
Ilustrasi radian dengan derajat dan sebaliknya :
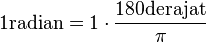
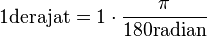
Contoh Soal dan Pembahasan
Luas Juring menggunakan perbandingan radian :
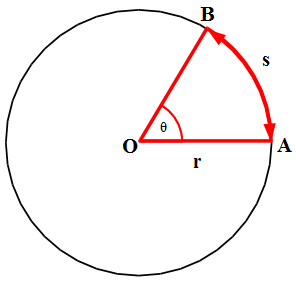
Kita akan mencari Luas AOB, dengan konsep radian : L. AOB/ L.Lingkaran = panjang AB/Keliling Lingkaran
Luas AOB/2πr2 = s/2πr
Luas AOB = ½ rs
karena s = rθ, maka
Luas AOB = ½ r2θ
Untuk membuat teman-teman lebih paham lagi, berikut kami berikan Contoh Soal dan Penyelesaianya
Contoh Soal 1
Nyatakan sudut 50° dan 89° ke dalam radian!
Penyelesian:
50° = 50° x π/180°
50° = 0,277π
50° = 0,277 (3,14)
50° = 0,87 radian
89° = 89° x π/180°
89° = 0,494π
89° = 0,494 (3,14)
89° = 1,55 radian
Contoh Soal 2
Nyatakan sudut 0,45 radian dan 0,89 radian ke dalam satuan derajat!
Penyelesaian:
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°
0,89 radian = 0,89 x 180°/π
0,89 radian = 51,02°
Contoh Soal 3
Sebuah kipas angin berputar dengan kecepatan 36 putaran per menit. Nyatakan kecepatan putaran kipas angin tersebut ke dalam satuan radian per detik!
Penyelesaian:
36 putaran/menit = 36 x 2π/60 putaran/detik
36 putaran/menit = 1,2π putaran/detik
Jadi 36 putaran per menit sama dengan 1,2π putaran per detik.
Contoh Soal 4
Hitunglah jari-jari suatu lingkaran jika panjang busurnya 10 cm dan sudut pusatnya 36°!
Penyelesaian:
θ = 36°, maka:
36° = 36°xπ/180°
36° = 0,2π
Kita ketahui bahwa :
r = s/θ
r = 10 cm/0,2π
r = 10 cm/0,628
r = 15,9 cm
Contoh Soal 5
Nyatakan besar sudut berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′
Penyelesaian:
a. kita ketahui bahwa:
1” = (1/3600)°
1′ = (1/60)°
1° = 0,0174 radian, maka:
30° 20′ 15”
= 30° + 20.(1/60)° + 15.(1/3600)°
= (108000/3600)° + (1200/3600)° + (15/3600)°
= (109215/3600)°
= (109215/3600).0,0174 radian
= 0,53 rad
b. kita ketahui bahwa:
1′ = (1/60)°
1° = 0,0174 radian, maka:
106° 20′ = 106° + 20.(1/60)°
106° 20′ = (318/3)° + (1/3)°
106° 20′ = (319/3)°
106° 20′ = (319/3).0,0174 radian
106° 20′ = 1,85 rad.
Sekian pembahasan tentang Materi Ukuran Derajat dan Ukuran Radian.
Semoga materi yang kami berikan menjadi referensi belajar yang bagus untuk teman-teman.


Sangat bemanfaat
Sangat Bermanfaat
Terimakasih sangat bermanfaat😊
Sama-sama kak 😀