Persamaan garis lurus menyatakan suatu persamaan yang mengartikan suatu garis lurus kedalam suatu persamaan.

Persamaan garis lurus yaitu salah satu cabang ilmu Matematika yang dipelajari sejak kita duduk di bangku SMP.

Persamaan ini, bisa diartikan juga dengan persamaan linier yaitu ada yang teriri dari satu variabel dan ada juga yang terdiri dari dua variabel.

Sebenarnya, apa itu persamaan garis lurus? Lalu, gimana rumus-rumusnya dan cara menentukannya? Yuk, simak ulasannya dibawah ini!

Pengertian Persamaan Garis Lurus

Perhatikan gambar diatas, beberapa contoh grafik dan bentuk garis lurus serta cara menyatakan atau menentukannya:

Persamaan garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang ada pada sebuah garis.

Sedangkan,

Garis lurus merupakan kumpulan dari titik-titik yang sejajar, dan garis lurus bisa dinyatakan dalam berbagai bentuk.

Dibawah ini, ada beberapa contoh untuk menyatakan persamaan garis lurus, yaitu:

• y = mx
• y = -mx
• y = a
• x = a
• ax + by = ab
• ax – by = -ab
• dan lain sebagainya.

Pengertian Gradien

Sebelum mempelajari lebih lanjut mengenai rumusnya. Kamu terlebih dahulu harus mengetahi 1 komponen yang tidak bisa terlepas dari persamaan garis lurus, yaitu Gradien.

Gradien yaitu suatu perbandingan komponen y dan juga komponen x , atau yang disebut juga dengan kecondongan sebuah garis. Simbol dari gradien yaitu berupa huruf  m.

atau,

Gradien juga bisa didefinisikan sebagai suatu nilai yang menyatakan kemiringan suatu garis. Pada umumnya, nilai gradien dari sebuah persamaan garis lurus dinyatakan lewat perbandingan Δy/Δx.

Coba kamu perhatikan cara untuk menentukan gradien pada gambar dibawah ini:

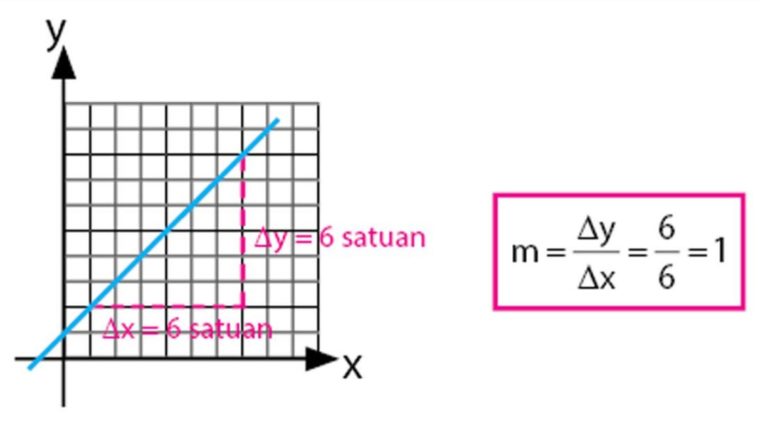
Cara buat menentukan gradien pada sebuah garis lurus dalam bidang kartesius juga bisa dipengaruhi oleh arah kemiringan garis tersebut.

Berikut, cara menentukan gradien garis pada pembahasan di bawah ini:

• Gradien dari persamaan nya ax + by + c = 0

M = komponen X / komponen Y

• Gradien yang melalui titik pusat nya ( 0, 0 ) dan titik ( a, b )

m = b / a

• Gradien yang melalui titiknya  ( x₁, y₁ ) dan ( x₂, y₂ )

m = y₁ – y₂ / x₁ – x₂ atau m = y₂ – y₁ / x₂ – x₁

• Gradien garis nya saling sejajar  ( / / )

m = sama atau apabila di simbolkan menjadi m₁ = m₂

• Gradien garis nya saling tegak lurus ( lawan dan kebalikan )

m = -1 atau  m₁ x m₂ = -1

Posisi Antara 2 Garis

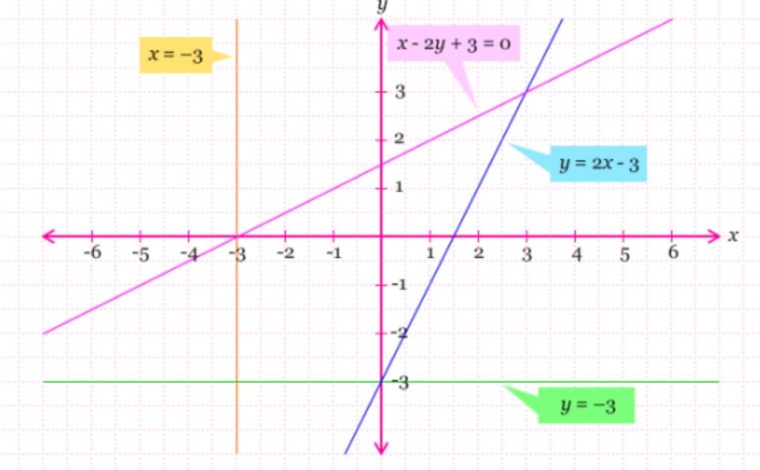
Posisi antara 2 garis pada persamaan garis lurus dibedakan menjadi 2, yaitu sejajar dan tegak lurus.

Dua posisi tersebut mempunyai persamaan garis lurus yang saling berkaitan.

Jadi, kalo ada 1 persamaan garis lurus yang diketahui, maka persamaan garis lurus yang saling sejajar atau tegak lurus dengan garis tersebut akan bisa diketahui.

Lalu, persamaan garis lurus itu memiliki syarat hubungan gradien. Syarat gradien dan gambar posisi antara 2 buah garis lurus seperti dibawah ini:

1. Garis yang Saling Sejajar

Garis sejajar yaitu dua buah garis yang tidak pernah akan memiliki titik potong. Dua buah garis yang saling sejajar ini memiliki gradien yang sama.

Diketahui gradien garis g = m_g dan gradien garis h = m_h. Jadi, hubungan antara gradien 2 buah persamaan garis itu bisa dinyatakan dalam persamaan dibawah ini:

m_g = m_h

2. Garis yang Saling Tegak Lurus

Gradien dari dua buah garis yang saling tegak lurus juga mempunyai hubungan.

Hubungan dari dua buah garis itu dinyatakan, kalo gradien garis kedua yaitu lawan dari kebalikan gradien garis yang pertama.

Atau dengan kata lain, juga bisa dikatakan kalo hasil dari perkalian 2 buah gradien tersebut sama dengan -1.

Contohnya: Gradien garis yang pertama memiliki nilai m₁ = 2, maka nilai dari gradien garis keduanya yaitu m₂ = -1/2.

Supaya kamu lebih memahami dengan lebih jelas, kamu bisa melihat pembahasannya di bawah ini:

Diketahui gradien garis g = m_g dan juga gradien garis h = m_h . Jadi, hubungan antara kedua gradien persamaan garis itu dinyatakan dalam persamaan seperti ini:

m_g x m_h = -1

Persamaan Garis Lurus

Suatu garis lurus bisa kamu ketahui persamannya melalui rumus dan juga sedikit perhitungan.

Tipe yang pertama, soal yang diketahui gradien dan juga satu titik potong. Sedangkan, buat tipe yang kedua yaitu persamaan yang diketahui dua titik potong.

Rumus untuk mencari persamaan garis itu akan kita bahas di bawah ini.

Ada 2 rumus yang bisa kamu gunakan dalam menentukan persamaan garis lurus. Pemakaian rumusnya bergantung pada apa yang diketahui di soal.

Simak kedua rumus tersebut pada ulasan berikut ini:

• Persamaan garis yang bergradien m dan melalui titik A(x₁.y₁)

y – y₁ = m(x – x₁)

• Persamaan garis yang melalui titik A(x₁.y₁) dan B(x₂.y₂)

y – y₁ / y₂ . y₁ = y – x₁ / x₂ . x₁

Rumus Persamaan Garis Lurus

1. Persamaan Garis Lurus Bentuk Umum (y = mx)

Persamaan yang melalui titik pusatnya (0,0) dan bergradien m.

Contohnya:

Tentukan persamaan dari garis lurus yang melalui titik pusat ( 0 , 0 ) dan juga bergradien 2!

Jawab:

• y = mx
• y = 2 x

2. Persamaan Garis Lurus Melalui Titik Sejajar (y = mx + c)

Persamaan garis lurus yang / / dengan y = mx dan bergradien m.

Persamaan garis lurus melalui titiknya (0,c) dan bergradien m. (0,c) merupakan titik potong sumbu y.

3. Persamaan Garis Lurus yang Melalui Titiknya (x₁ , y₁) dan Bergradien m

Persamaannya yaitu sebagai berikut ini:

y – y₁ = m (x – x₁)

4. Persamaan Garis Lurus yang Melalui 2 Titik (x₁ , y₁ ) dan ( x₂ , y₂ )

Persamaannya yaitu sebagai berikut ini:

y – y₁ / y₂ – y₁ = x – x₁ / x₂ – x₁

Contoh Soal Persamaan Garis Lurus

1. Tentukan persamaan dari garis lurus yang meleati titik potong garis-garis dengan persaamaan 3x + 2y – 12 dan 5x + 2y = 16 dan sejajar dengan garis 2x + y = 4 yaitu?

Jawab:

3x + 2y = 12
5x + 2y = 16
___________-
-2x = -4
x = -4 / -2 = 2

3x + 2y  = 12
3 x 2 + 2y = 12
6 + 2y = 12
2y = 6
y = 6/2 = 3

Titik potongnya (2, 3) // 2x + y = 4

m₁ = -a / b = -2 / 1 = -2

m₁ = m₂ = -2

y – y₁ = m₂ ( x – x₁ )

y – 3 = -2 ( x – 2 )

y – 3 = -2x + 4

2x + y – 3 + 4 = 0

2x + y + 1 = 0

2. Persamaan garis lurus yang melalui titik A(-2, -3) dan tegak lurus terhadap garis dengan persamaan y = 2/3x + 9 adalah?

Jawab:

Mencari gradien garis y = 2/3x + 9:

m₁ = 2/3x

Suatu garis akan tegak lurus dengan suatu persamaan garis apabila memiliki gradien yang memenuhi:

m₁ x m₂ = -1

2/3 x m₂ = -1

m₂ = -1/ 2/3

m₂ = -3/2

Berikutnya, akan dicari persamaan garis dengan gradien m₂ = -3/2 yang melewati titik (-2, -3)

y – y₁ = m₂ ( x – x₁ )

y – (-3) = -3/2 ( x – (-2))

y + 3 = -3/2 (x + 2)

2(y + 3) = -3 (x + 2)

2y + 6 = -3x – 6

2y + 3x + 6 + 6 = 0

2y + 3x + 12 = 0

3x + 2y + 12 = 0

Jadi, persamaan garis lurus diatas adalah 3x + 2y + 12 = 0

Semoga materi tentang Persamaan Garis Lurus lengkap dengan contoh soalnya bermanfaat untuk teman-teman.

Jangan lupa untuk selalu kunjungi cerdika.com ya! Selamat belajar 😀