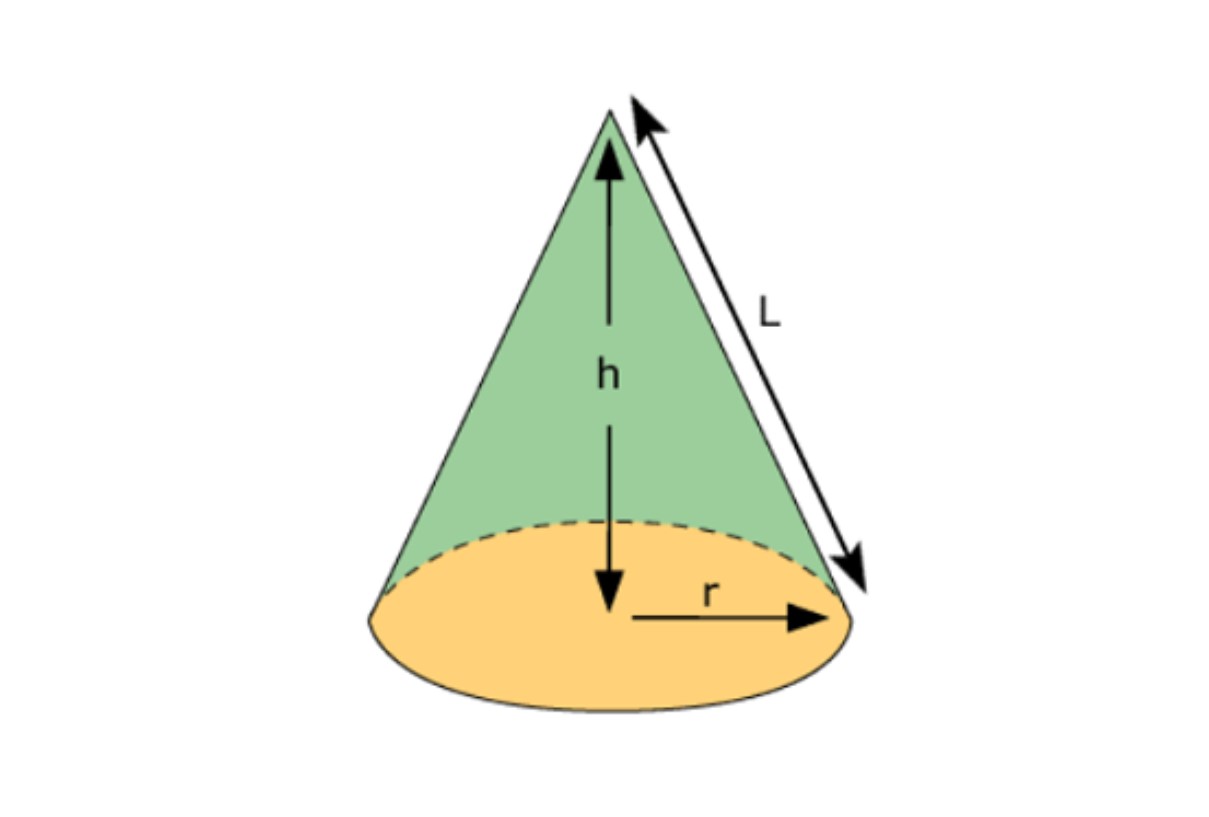
Apa sih, yang dimaksud dengan bangun ruang Kerucut itu?
Kerucut adalah bangun ruang yang memiliki 2 sisi, yaitu sebuah lingkaran dan juga sebuah bidang lengkung.
Atau, juga dikenal dengan limas yang memiliki alas berbentuk lingkaran.
Secara umum, lingkaran pada kerucut bertindak sebagai alas dan bidang lengkung menunjuk sebuah titik yang merupakan puncak kerucut.
Kerucut merupakan salah satu jenis limas yang istimewa dan dalam bahasa inggris disebut “Cone”.
Kerucut bisa dibentuk dari sebuah segitiga siku-siku yang diputar sejauh 360o, dimana sisi siku-sikunya sebagai pusat putaran.
Ingin tahu lebih lengkap mengenai Rumus Kerucut? Yuk, langsung simak pembahasan dibawah ini.
Sifat-Sifat Kerucut
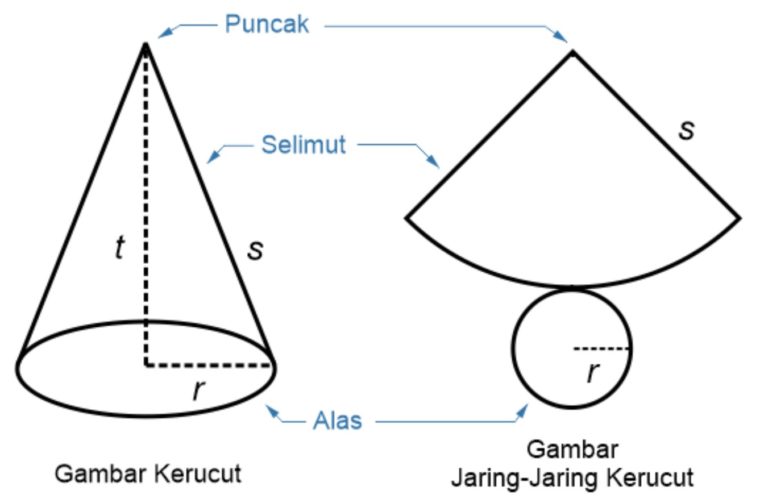
Berikut dibawah ini, ada beberapa sifat-sifat kerucut yang perlu kamu ketahui, diantaranya yaitu:
- Tersusun oleh 2 buah sisi, yaitu lingkaran dan sebuah sisi lengkung.
- Sisi yang berbentuk lingkaran merupakan alas kerucut.
- Sisi yang berbentuk bidang lengkung membentuk selimut kerucut.
- Bidang lengkung pada kerucut merupakan juring lingkaran (sektor).
- Kerucut mempunyai 1 rusuk dan 1 titik puncak.
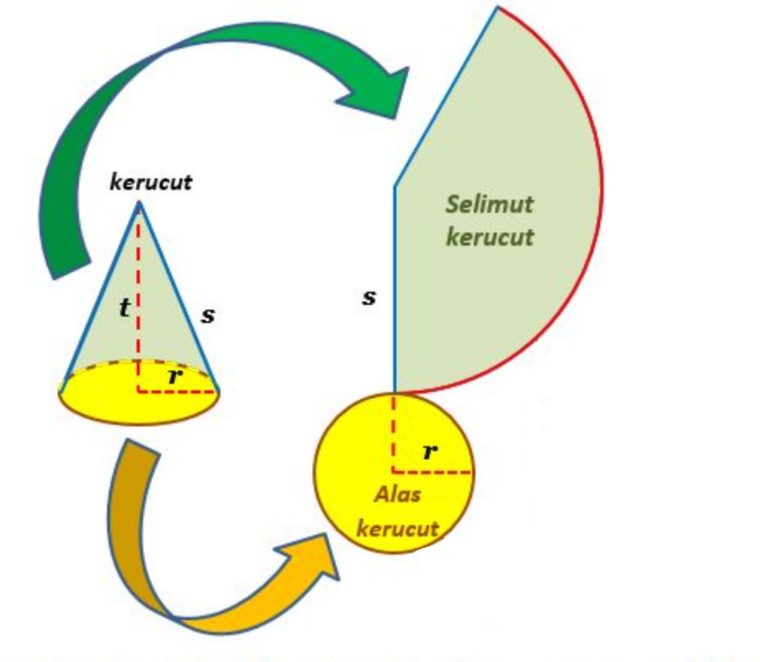
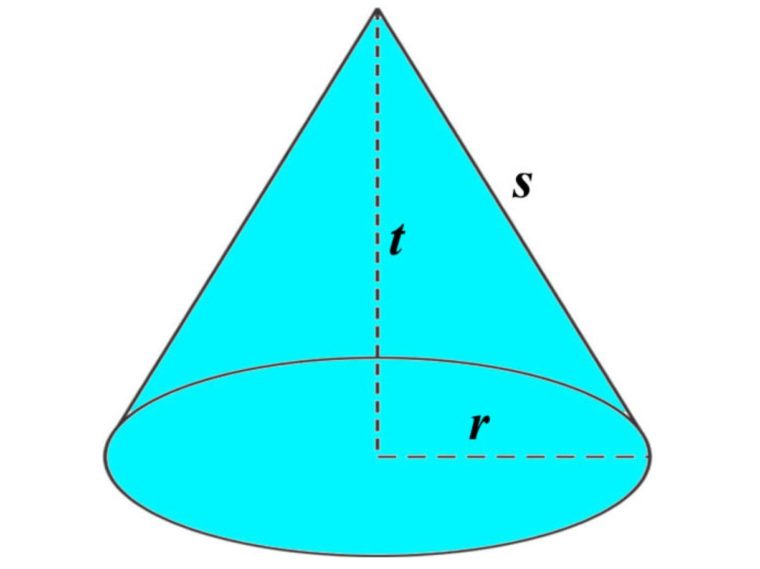
Unsur-Unsur Kerucut
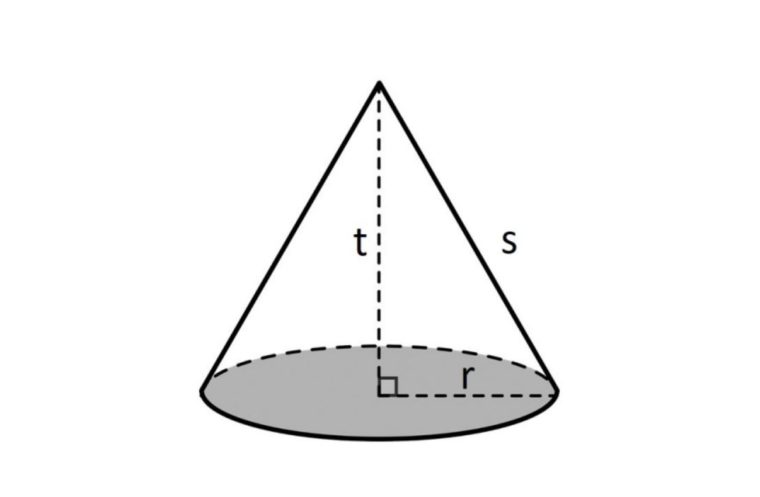
Kerucut memiliki beberapa unsur-unsur didalamnya, diantaranya seperti dibawah ini:
- Bidang Alas : Yaitu sisi yang berbentuk lingkaran (daerah yang diraster) dengan pusat di titik O.
- Diameter Bidang Alas (d) : Merupakan ruas garis AB.
- Jari-Jari Bidang Alas (r) : Merupakan ruas garis OA dan rua garis OB.
- Tinggi Kerucut (t) : Yaitu jarak dan titik puncak kerucut C ke pusat bidang alas O, adalah ruas garis CO.
- Selimut Kerucut : Yaitu sisi kerucut yang tidak diraster yang merupakan bidang lengkung.
- Apotema atau Garis Pelukis (s) : Merupakan sisi miring BC.
Rumus Kerucut
1. Rumus Volume Kerucut
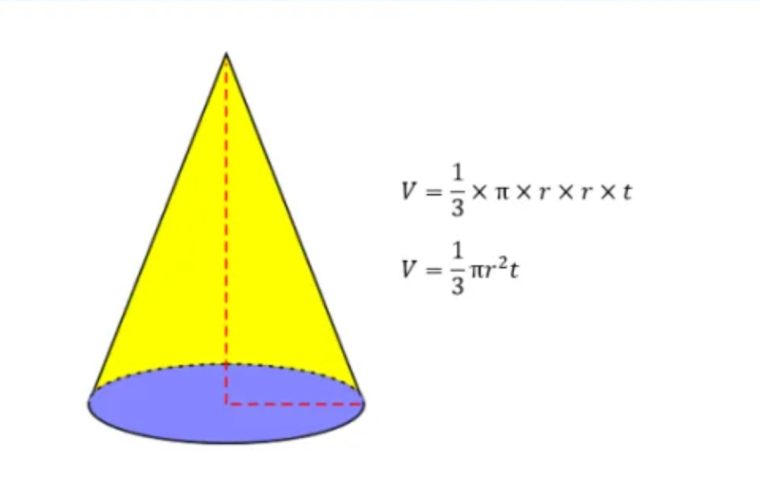
Rumusnya:
V = 1/3 x π x r x r x t
atau,
V = 1/3 πr²t
Keterangan:
- V = Volume bangun kerucut
- r = Jari-jari bangun kerucut
- t = Tinggi bangun kerucut
- π = 22/7 atau 3,14
2. Rumus Luas Permukaan Kerucut
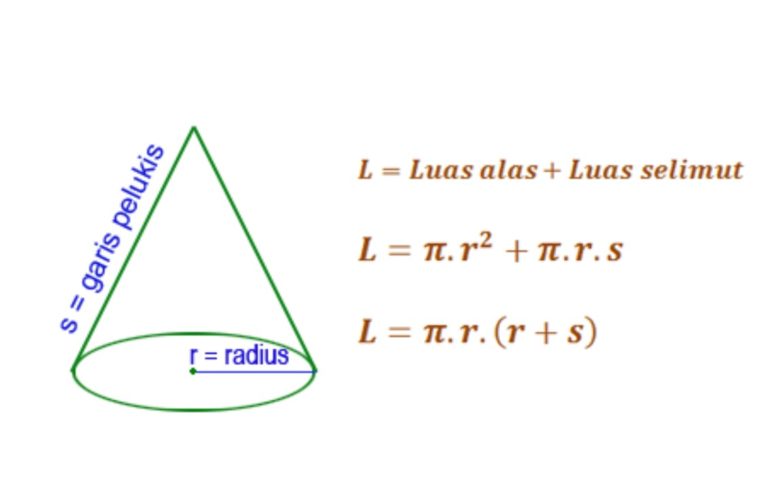
Rumusnya:
L = La + Ls
= (π x r²) + (π x r x s)
= π x r x (r + s)
Keterangan:
- L = Luas permukaan kerucut
- La = Luas alas kerucut
- Ls = Luas selimut kerucut
- r = Jari-jari bangun kerucut
- s = Panjang garis pelukis (apotema) kerucut
- π = 22/7 atau 3,14
3. Rumus Luas Alas Kerucut
Rumusnya:
La = π x r x r
= π x r²
Keterangan:
- La = Luas alas kerucut
- r = Jari-jari bangun kerucut
- π = 22/7 atau 3,14
4. Rumus Luas Selimut Kerucut
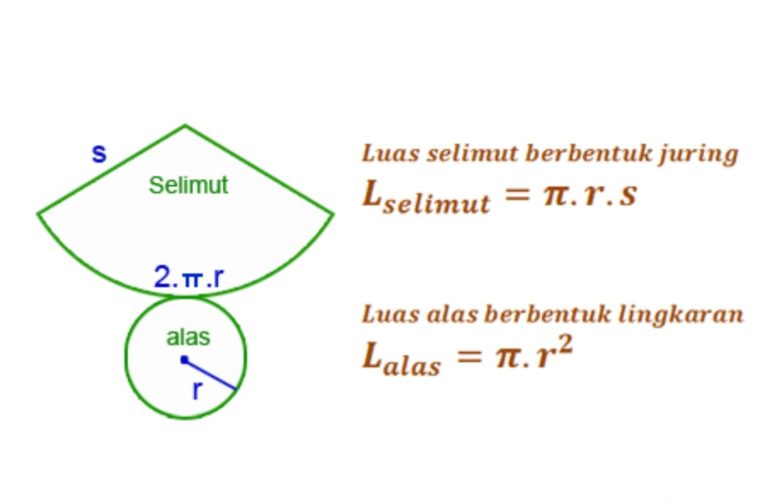
Rumusnya:
Ls = π x r x s
Keterangan:
- Ls = Luas selimut bangun kerucut
- r = Jari-jari bangun kerucut
- s = Panjang garis pelukis (apotema) kerucut
- π = 22/7 atau 3,14
5. Rumus Jari-Jari Kerucut
Rumus jari-jari kerucut ini terbagi menjadi beberapa, yaitu:
Rumus jari-jari (r) diketahui V:
r = √(3 x V) / (π x t)
Jari-jari (r) diketahui L:
Faktor dari
r² + rs – (L/π) = 0
Jari-jari (r) diketahui Ls:
r = Ls / (π x s)
Keterangan:
- L = Luas permukaan kerucut
- V = Volume kerucut
- Ls = Luas selimut kerucut
- r = Jari-jari bangun kerucut
- s = Panjang garis pelukis (apotema) kerucut
- π = 22/7 atau 3,14
6. Rumus Tinggi Kerucut
Rumusnya:
t = (3 x V) / (π x r x r)
Keterangan:
- t = Tinggi bangun kerucut
- V = Volume bangun kerucut
- r = Jari-Jari bangun kerucut
- π = 22/7 atau 3,14
Contoh Soal Rumus Kerucut

1. Sebuah lingkaran memiliki luas 40 cm². Kalo lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm. Maka, hitunglah volume kerucut tersebut!
Jawab:
Diketahui:
- t = 9 cm
- L = π x r² = 40 cm²
Ditanya:
- Volume kerucut (V) …?
Dijawab:
- V = 1/3 x π x r² x t
- V = 1/3 x 40 x 9 (ingat: π x r² = 40 cm²)
- = 120 cm³.
Sehingga, volume sebuah bangun kerucut tersebut adalah 120 cm³.
2. Jika diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm. Tentukanlah panjang apotema (s), luas selimut kerucut, luas permukaan!
Jawab:
Diketahui:
- d = 10, maka r = 5 cm
- t = 12 cm
Ditanya:
- Panjang garis pelukis (s)?
- Luas selimut kerucut?
- Luas permukaan kerucut?
Dijawab:
a. Panjang Garis Pelukis (s):
- s2 = t2 + r2
- = 122 + 52
- = 144 + 25 = 169
- s = 13
Jadi, panjang garis pelukis kerucut tersebut adalah 13 cm.
b. Luas Selimut Kerucut:
- Ls = π x r x s
- Ls = 3,14 x 5 x 13
- = 204,1 cm2
Jadi, luas selimut kerucut tersebut adalah 204,1 cm2.
c. Luas Permukaan Kerucut:
- L = = π x r x (r + s)
- L = 3,14 x 5 x (13 + 5)
- L = 282, 6 cm2
Sehingga, luas permukaan kerucut tersebut adalah 282, 6 cm2.
3. Hitunglah jari-jari kerucut yang mempunyai tinggi 20 cm dan luas permukaan 2640 cm².
Jawab:
Diketahui:
- t = 20 cm
- L = 2640 cm²
Ditanya:
- Jari-jari kerucut (r) …?
Dijawab:
Untuk dapat membentuk faktor persamaan, dihitung dulu panjang garis pelukis (s):
- s = √r² + t²
- s = √(21 cm)² + (20 cm)²
- s = √441 cm² + 400 cm²
- s = √841 cm²
- s = 29 cm
Selanjutnya, substitusi nilai s = 29 ke persamaan berikut ini:
- r² + rs – (L/π) = 0
- r² + 29r – 2640/(22/7) = 0
- r² + 29r – (7 x 2640)/22 = 0
- r² + 29r – 840 = 0
- (r + 40)(r – 21) = 0
- r = -40 dan r = 21
Dari hasil faktor persamaan dapat diuji:
- r = -40 cm tidak memenuhi syarat, karena hasil luas permukaan akan bernilai negatif atau tidak sama 2640 cm²
- r = 21 cm memenuhi syarat, karena hasil hasil luas permukaan bernilai 2640 cm².
Jadi, jari-jari kerucut tersebut adalah 21 cm.
4. Hitunglah tinggi kerucut yang mempunyai jari-jari 5 cm dengan volume 157 cm³.
Jawab:
Diketahui:
- r = 5 cm
- V = 157 cm³
Ditanya:
- Tinggi kerucut (t) …?
Dijawab:
Karena r bukan kelipatan 7, maka digunakan π = 3,14
- t = (3 x V) / (π x r x r)
- t = (3 x 157 cm³) / (3,14 x 5 cm x 5 cm)
- t = 471 cm³ / 78,5 cm²
- t = 6 cm
Sehingga, tinggi sebuah bangun kerucut tersebut adalah 6 cm.
Gimana pembahasan diatas? Sangat mudah buat dipahami dan dipelajari kan?
Terima kasih teman-teman sudah membaca tentang Rumus Bangun Ruang Kerucut diatas tadi.
Semoga bisa membantu dan bermanfaat. Jangan lupa juga untuk selalu kunjungi cerdika.com yak 😀